Duda chorra, o no, acerca de probabilidad aplicada al Poker.
8 años 3 meses
4
Hola chicos.
Voy a plantear dos escenarios los cuales sabemos, pero no quizás una explicación mas detallada y el porque de que asi sea. Por lo que me gustaria pedir a los entendidos del tema una explicación concisa.
Imaginamos que vamos allin en flop con 15 outs favorables para ganar, lo que nos daria alrededor o más del 55% de las veces.
¿Porque si al rival le sirven el resto de outs no ganará un % mayor?
Y la siguiente pregunta es imaginando la misma situación pero en su lugar haremos "RunitTwice" y con la condición de no dividir el bote. Aqui sabremos que deberiamos ganar el 100% de las veces usando el mismo calculo, pero a la misma vez sabiendo que no sucederá ese 100% en determinados casos aislados, con lo cual el % real deberia ser algo mas del 90%?
Esto es cuando uno se pone a divagar en estas cosas y surgen mas porques de lo que en un principio sabemos de sobra.
Muchas gracias por los aportes!
11 años 8 meses
1.999
No entiendo cómo aplicas run it twice sin partir el bote ¿si ganas uno y pierdes otro?
8 años 3 meses
4
Me referia a imaginarnos que solo nos jugamos un bote pero con la condicion de tirar dos turns y dos rivers por asi decirlo, o independientemente de si partimos el bote, cual es la probabilidad total de ligar nuestra combinación pero teniendo dos cartas mas por descubrir.
8 años 3 meses
4
Os voy a exponer este ejemplo para que veais claramente cual es mi duda y a ver si alguien me ilumina 😄
Imaginemos el mazo de 52 cartas que posee 4 palos.
Ahora elegimos cualquier carta al azar y sabemos que tenemos un 25% de probabilidades de que sea una pica por ejemplo.
Bien, hasta aqui todos de acuerdo. El tema es, que probabilidades hay de que haya una pica si elegimos 2 cartas, 3 o 4?
1 carta = 25%
2 cartas = 50% ( deberia ser aproximado )
3 cartas = 75% ( " )
4 cartas = 100 % ( " )
Espero que se me haya entendido gracias por las respuestas!
11 años 8 meses
1.999
Tus outs dividido las cartas que quedan en el mazo te da el % de salir en la siguiente calle. En la siguiente calle vas a tener la misma operación pero el mazo va a tener 1 carta menos, sumas los porcentajes y listo.
Con el segundo ejemplo lejos de exponer claramente tu duda estoy mas desorientado y no se la respuesta que quieres encontrar aunque lo que está claro es que mientras haya otros palos en la baraja la posibilidad de que salga pica nunca va a ser del 100%.
12 años 2 meses
2.560
Contestando a la segunda duda del OP:
La probabilidad de 1 carta y que sea pica es 13/52= 0.25
La de robar 2 cartas y que almenos 1 sea pica es: 13/52 + (39/52 x 13/51)= 0.44
La de robar 3 cartas y que almenos 1 sea picas es: 13/52 + (39/52 x 13/51) + (39/52 x 38/51 x 13/50) = 0.59
Y así hasta que robes 14 cartas o más donde será 100%
Para que te quede más claro, piensa que no solo se suman las probabilidades de que te salga pica. Se resta la probabilidad de que no te salga.
Piensa en cara o cruz. Que tires dos veces una moneda no te garantiza una Cara.
Posibilidades.4:
1. Cara-Cara
2. Cara-Cruz
3. Cruz-Cara
4. Cruz-Cruz
Si ves los casos. La cara aparece en 3 de los 4 casos. Así que tienes un 0.75
8 años 3 meses
4
Gracias!
No me queda muy claro o no entiendo bien que a partir de robar la decimocuarta carta sea la probabilidad el 100%, el 100% absoluto no seria a partir de la carta numero 39?
12 años 2 meses
2.560
Tienes razón. Me he equivocado.
Además es más fácil calcular la probabilidad de que salga No-picas las 3 veces y restarlo a 1. Aunque el resultado es el mismo.
Ya que estamos lo aplicamos a tu primera pregunta.
Si tienes un 55%, la probailidad de que ganes alguno de los dos flops sería 1- 0.45x0.45= 0.7975
11 años 1 mes
3.143
AlwaysImproImaginamos que vamos allin en flop con 15 outs favorables para ganar, lo que nos daria alrededor o más del 55% de las veces.
¿Porque si al rival le sirven el resto de outs no ganará un % mayor?
Porque solo necesitamos que salga alguna de nuestras outs en 1 de las 2 calles, y el rival necesita que salgan sus outs en las 2 calles.
12 años 2 meses
2.560
Perdón. Sino entendía bien tu duda.
Si tienes un 80% y hay un run it twice, las probabilidades de ganar los dos boards sería un 0.64 aprox.
La probabilidad de ganar sólo uno es un 0.32 y perder los dos es un 0.04
9 años 3 meses
138
Y la de ganar al menos uno de los dos es un 0.96%.
P(A+B) = P(A) + P(B) - P(A^B) (intersección) --> 80% + 80% - 64% = 96%
También sirve la que usaron antes, P(A+B) = 1 - (1-P(A) * 1-P(B)) --> 1 - (20% * 20%) = 1 - 0.04 = 0.96
Son equivalentes.
En el caso de los 15 outs y el 55%: 55% + 55% - (55%*55%) = 0.7975.
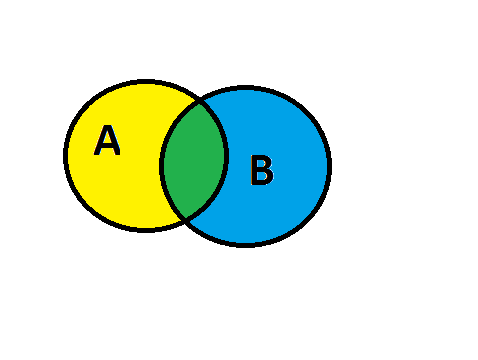
Si para calcular la probabilidad de la unión de dos sucesos sumas directamente, lo que estás haciendo es sumar dos veces la probabilidad de la intersección, en el dibujito (un diagrama de Venn), estarías sumando dos veces la zona verde, que es la probabilidad de que caiga uno de outs en las dos calles, en turn Y en river, de ahí el error.
