legitimidad de stats
16 años
1.657
A partir de que cantidad de manos los siguientes stats se pueden considerar como veridicos?
Vpip y PFR
Steal
Agg% por calles y AF TOTAL
fold de sb y bb ante intento de robo.
Fold to bet flop
cbet
fold to 3 bet y 4bet(aunque ya me comento dargor que aqui serian aprox 500 manos).
16 años
1.657
tan dificil es esta pregunta?
18 años
181
vpip/pfr a partir de 200 manos ya tienes una idea muy aproximada a como es ese jugador, para steal, agg%, cbet, f tobet flop y demas stats que se dan postflop y steals, yo empezaria a tomarlas un poco en serio a partir de las 600 y stats de fold 3bet/4bet y postflop en ultimas calles para tener datos algo mas reales a partir de las 1000 manos.
Estos valores los considero aproximados, cuando menos se de una situacion logicamente más manos necesitaremos para que esa stats sea realista, por ej fold 3bet por calle necesitariamos muchisimas manos para tener un valor real.
20 años
11.048
16 años
1.657
tan dificil es esta pregunta?
Rastrilltan dificil es esta pregunta?
más de lo que parece. Pero más difícil es ganar a esto sin tener paciencia.
18 años
2.413
Vpip y PFR
100, 200 por ahí
Steal
Agg% por calles y AF TOTAL
fold de sb y bb ante intento de robo.
Fold to bet flop
cbet
fold to 3 bet y 4bet
sobre las 1000 o más
17 años
6.442
vpip y pfr en 100 manos es suficiente, pero ya en 50 podes llegar a saber si es un fish o no
la aff y af en 500 manos y ya solo son una tendencia, pero no son muy reales
la cb en 200 manos ya tiende
y el resto a partir como dijeron de 1000 manos
igualmente, te recomiendo que te fijes en cuantos casos ocurre, porque un fold4bet en 2000 manos tal vez ocurrió 2 veces y por supuesto no es fiable
en especial el fold 4bet te diría 5k para arriba
saludos
pd. un poco de paciencia hombre
17 años
1.842
En 10 manos ya se sabe si un jugador es un fish o no
19 años
10.037
17 años
1.842
En 10 manos ya se sabe si un jugador es un fish o no
durango198En 10 manos ya se sabe si un jugador es un fish o no
Se puede saber en una mano también. :D
16 años
1.626
Rastrillfold to 3 bet y 4bet(aunque ya me comento dargor que aqui serian aprox 500 manos).
De buen fish te vas a fiar tu... Del fold 3bet si que puedes ir mirando a partir de 500 manos (pero sin tampoco darle 100% de credibilidad). Lo del 4bet me extraña haberlo dicho, ahí si que necesitas miles de manos para tener rangos creíbles y esa si que es una stat que, de usar, ha de saberse a ciencia cierta.
16 años
1.792
Debido a una discusión que se armó en otro hilo sobre la validez o no justamente de uno de los datos por el que preguntas (attempt to steal) me he puesto a pensar justamente sobre que cantidad de manos o muestras esas estadísticas estarán mostrando un valor que tenga algún sentido y me he puesto a hacer algunos cálculos y estimaciones.
No tengo esto del todo procesado por lo que mas bien será un brain storming y no un post organizado (seguramente será un ladrillo je).
Como dije esto no está previamente ordenado asi que voy escribiendo a medida que me van surgiendo las ideas.
Supongamos el lanzamiento de una moneda. Asumimos que tanto cara como número tienen la misma probabilidad de ocurrencia (50%).
Si nos preguntamos por ejemlpo cual es la probabilidad de que en 5 lanzamientos consecutivos salga siempre cara, pues la respuesta es sencilla: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Ahora bien, tratemos de involucrar al poker para obtener un resultado similar.
Supongamos un jugador que tenemos en varios miles de manos con un attempt to steal desde SB = 50%. Como se trata de varios miles de manos pues asumimos que el dato se aproxima a la realidad casi sin error.
Ahora bien, que ocurre si queremos calcular la probabilidad de que en una muestra de solamente 5 intentos este jugador intente robar las ciegas todas las veces?
Supongamos por un instante que el jugador decide solamente en función de sus cartas, separa el rango en 50-50 y si le toca una combinación dentro del 50% superior entonces hará el raise y si le toca una combinación dentro del 50% inferior foldeará.
Bajo esa hipótesis la probabilidad de ocurrencia de 5 intentos consecutivos de robo es la misma que en el caso del lanzamiento de la moneda: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Pero que diferencia hay entre el poker y el lanzamiento de la moneda?
Pues en mi opinión que un jugador de poker no decide si hacer o no hacer el raise solamente basado en el rango de su mano, mas bien diría que es mas importante el conocimiento de las estadísticas del villano en BB que sus propias cartas.
A que apunto con esto? A que dadas determinadas condiciones (por ejemplo un villano en BB con un elevado fold al attempt to steal desde SB) es mas probable ocurrencias de 5 raises consecutivos en el poker a pesar de que el jugador tenga un 50% de attempt to steal que en el ejemplo del lanzamiento de la moneda. Y obviamente también ocurre a la inversa y es mas probable encontrar secuencias de 5 folds consecutivos en el poker para un jugador con 50% de attempt to steal que nuevamente el ejemplo de la moneda.
Dicho de otra manera, la campana parecería estar mas achatada para el poker que para situaciones que no se ven afectadas por situaciones externas (como es el lanzamiento de la moneda). Esto hace que sea necesario una muestra mayor para darle valor a las estadísticas de la que se necesitaría para verificar por ejemplo la probabilidad de ocurrencia en un lanzamiento (asumiendo que el lanzamiento no se ve afectado por agentes externos).
De todas formas y para simplificar un poco los cálculos, y sobre todo porque no se como mensurar ese achatamiento haré una aproximación al cálculo asumiendo un comportamiento que es ajeno a los componentes externos (básicamente la composición de villanos de la mesa).
(Sigue en próximo post mientras ordeno un poco las ideas)
17 años
4.367
16 años
1.792
Debido a una discusión que se armó en otro hilo sobre la validez o no justamente de uno de los datos por el que preguntas (attempt to steal) me he puesto a pensar justamente sobre que cantidad de manos o muestras esas estadísticas estarán mostrando un valor que tenga algún sentido y me he puesto a hacer algunos cálculos y estimaciones.
No tengo esto del todo procesado por lo que mas bien será un brain storming y no un post organizado (seguramente será un ladrillo je).
Como dije esto no está previamente ordenado asi que voy escribiendo a medida que me van surgiendo las ideas.
Supongamos el lanzamiento de una moneda. Asumimos que tanto cara como número tienen la misma probabilidad de ocurrencia (50%).
Si nos preguntamos por ejemlpo cual es la probabilidad de que en 5 lanzamientos consecutivos salga siempre cara, pues la respuesta es sencilla: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Ahora bien, tratemos de involucrar al poker para obtener un resultado similar.
Supongamos un jugador que tenemos en varios miles de manos con un attempt to steal desde SB = 50%. Como se trata de varios miles de manos pues asumimos que el dato se aproxima a la realidad casi sin error.
Ahora bien, que ocurre si queremos calcular la probabilidad de que en una muestra de solamente 5 intentos este jugador intente robar las ciegas todas las veces?
Supongamos por un instante que el jugador decide solamente en función de sus cartas, separa el rango en 50-50 y si le toca una combinación dentro del 50% superior entonces hará el raise y si le toca una combinación dentro del 50% inferior foldeará.
Bajo esa hipótesis la probabilidad de ocurrencia de 5 intentos consecutivos de robo es la misma que en el caso del lanzamiento de la moneda: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Pero que diferencia hay entre el poker y el lanzamiento de la moneda?
Pues en mi opinión que un jugador de poker no decide si hacer o no hacer el raise solamente basado en el rango de su mano, mas bien diría que es mas importante el conocimiento de las estadísticas del villano en BB que sus propias cartas.
A que apunto con esto? A que dadas determinadas condiciones (por ejemplo un villano en BB con un elevado fold al attempt to steal desde SB) es mas probable ocurrencias de 5 raises consecutivos en el poker a pesar de que el jugador tenga un 50% de attempt to steal que en el ejemplo del lanzamiento de la moneda. Y obviamente también ocurre a la inversa y es mas probable encontrar secuencias de 5 folds consecutivos en el poker para un jugador con 50% de attempt to steal que nuevamente el ejemplo de la moneda.
Dicho de otra manera, la campana parecería estar mas achatada para el poker que para situaciones que no se ven afectadas por situaciones externas (como es el lanzamiento de la moneda). Esto hace que sea necesario una muestra mayor para darle valor a las estadísticas de la que se necesitaría para verificar por ejemplo la probabilidad de ocurrencia en un lanzamiento (asumiendo que el lanzamiento no se ve afectado por agentes externos).
De todas formas y para simplificar un poco los cálculos, y sobre todo porque no se como mensurar ese achatamiento haré una aproximación al cálculo asumiendo un comportamiento que es ajeno a los componentes externos (básicamente la composición de villanos de la mesa).
(Sigue en próximo post mientras ordeno un poco las ideas)
luzipheDebido a una discusión que se armó en otro hilo sobre la validez o no justamente de uno de los datos por el que preguntas (attempt to steal) me he puesto a pensar justamente sobre que cantidad de manos o muestras esas estadísticas estarán mostrando un valor que tenga algún sentido y me he puesto a hacer algunos cálculos y estimaciones.
No tengo esto del todo procesado por lo que mas bien será un brain storming y no un post organizado (seguramente será un ladrillo je).
Como dije esto no está previamente ordenado asi que voy escribiendo a medida que me van surgiendo las ideas.
Supongamos el lanzamiento de una moneda. Asumimos que tanto cara como número tienen la misma probabilidad de ocurrencia (50%).
Si nos preguntamos por ejemlpo cual es la probabilidad de que en 5 lanzamientos consecutivos salga siempre cara, pues la respuesta es sencilla: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Ahora bien, tratemos de involucrar al poker para obtener un resultado similar.
Supongamos un jugador que tenemos en varios miles de manos con un attempt to steal desde SB = 50%. Como se trata de varios miles de manos pues asumimos que el dato se aproxima a la realidad casi sin error.
Ahora bien, que ocurre si queremos calcular la probabilidad de que en una muestra de solamente 5 intentos este jugador intente robar las ciegas todas las veces?
Supongamos por un instante que el jugador decide solamente en función de sus cartas, separa el rango en 50-50 y si le toca una combinación dentro del 50% superior entonces hará el raise y si le toca una combinación dentro del 50% inferior foldeará.
Bajo esa hipótesis la probabilidad de ocurrencia de 5 intentos consecutivos de robo es la misma que en el caso del lanzamiento de la moneda: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Pero que diferencia hay entre el poker y el lanzamiento de la moneda?
Pues en mi opinión que un jugador de poker no decide si hacer o no hacer el raise solamente basado en el rango de su mano, mas bien diría que es mas importante el conocimiento de las estadísticas del villano en BB que sus propias cartas.
A que apunto con esto? A que dadas determinadas condiciones (por ejemplo un villano en BB con un elevado fold al attempt to steal desde SB) es mas probable ocurrencias de 5 raises consecutivos en el poker a pesar de que el jugador tenga un 50% de attempt to steal que en el ejemplo del lanzamiento de la moneda. Y obviamente también ocurre a la inversa y es mas probable encontrar secuencias de 5 folds consecutivos en el poker para un jugador con 50% de attempt to steal que nuevamente el ejemplo de la moneda.
Dicho de otra manera, la campana parecería estar mas achatada para el poker que para situaciones que no se ven afectadas por situaciones externas (como es el lanzamiento de la moneda). Esto hace que sea necesario una muestra mayor para darle valor a las estadísticas de la que se necesitaría para verificar por ejemplo la probabilidad de ocurrencia en un lanzamiento (asumiendo que el lanzamiento no se ve afectado por agentes externos).
De todas formas y para simplificar un poco los cálculos, y sobre todo porque no se como mensurar ese achatamiento haré una aproximación al cálculo asumiendo un comportamiento que es ajeno a los componentes externos (básicamente la composición de villanos de la mesa).
(Sigue en próximo post mientras ordeno un poco las ideas)
toma otro ladrillo... pa la colección, a este paso nos hacemos un adosadito. juassssssssss
20 años
21.808
16 años
1.792
Debido a una discusión que se armó en otro hilo sobre la validez o no justamente de uno de los datos por el que preguntas (attempt to steal) me he puesto a pensar justamente sobre que cantidad de manos o muestras esas estadísticas estarán mostrando un valor que tenga algún sentido y me he puesto a hacer algunos cálculos y estimaciones.
No tengo esto del todo procesado por lo que mas bien será un brain storming y no un post organizado (seguramente será un ladrillo je).
Como dije esto no está previamente ordenado asi que voy escribiendo a medida que me van surgiendo las ideas.
Supongamos el lanzamiento de una moneda. Asumimos que tanto cara como número tienen la misma probabilidad de ocurrencia (50%).
Si nos preguntamos por ejemlpo cual es la probabilidad de que en 5 lanzamientos consecutivos salga siempre cara, pues la respuesta es sencilla: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Ahora bien, tratemos de involucrar al poker para obtener un resultado similar.
Supongamos un jugador que tenemos en varios miles de manos con un attempt to steal desde SB = 50%. Como se trata de varios miles de manos pues asumimos que el dato se aproxima a la realidad casi sin error.
Ahora bien, que ocurre si queremos calcular la probabilidad de que en una muestra de solamente 5 intentos este jugador intente robar las ciegas todas las veces?
Supongamos por un instante que el jugador decide solamente en función de sus cartas, separa el rango en 50-50 y si le toca una combinación dentro del 50% superior entonces hará el raise y si le toca una combinación dentro del 50% inferior foldeará.
Bajo esa hipótesis la probabilidad de ocurrencia de 5 intentos consecutivos de robo es la misma que en el caso del lanzamiento de la moneda: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Pero que diferencia hay entre el poker y el lanzamiento de la moneda?
Pues en mi opinión que un jugador de poker no decide si hacer o no hacer el raise solamente basado en el rango de su mano, mas bien diría que es mas importante el conocimiento de las estadísticas del villano en BB que sus propias cartas.
A que apunto con esto? A que dadas determinadas condiciones (por ejemplo un villano en BB con un elevado fold al attempt to steal desde SB) es mas probable ocurrencias de 5 raises consecutivos en el poker a pesar de que el jugador tenga un 50% de attempt to steal que en el ejemplo del lanzamiento de la moneda. Y obviamente también ocurre a la inversa y es mas probable encontrar secuencias de 5 folds consecutivos en el poker para un jugador con 50% de attempt to steal que nuevamente el ejemplo de la moneda.
Dicho de otra manera, la campana parecería estar mas achatada para el poker que para situaciones que no se ven afectadas por situaciones externas (como es el lanzamiento de la moneda). Esto hace que sea necesario una muestra mayor para darle valor a las estadísticas de la que se necesitaría para verificar por ejemplo la probabilidad de ocurrencia en un lanzamiento (asumiendo que el lanzamiento no se ve afectado por agentes externos).
De todas formas y para simplificar un poco los cálculos, y sobre todo porque no se como mensurar ese achatamiento haré una aproximación al cálculo asumiendo un comportamiento que es ajeno a los componentes externos (básicamente la composición de villanos de la mesa).
(Sigue en próximo post mientras ordeno un poco las ideas)
luziphe
(Sigue en próximo post mientras ordeno un poco las ideas)
Te voy a ahorrar un poco de trabajo: Intervalo de confianza.
O bueno, ahora que veo el artículo igual te supone más trabajo, pero vamos, que esto de saber cómo de fiable es un dato basado en cierta muestra ya existe y es de lo más básico del primer curso de estadística de cualquier carrera de números.
16 años
1.792
Tratando de contestar sobre la pregunta del hilo, en mi opinión todas las estadísticas necesitan una cantidad similar de muestras para ser fiables (estoy haciendo alguna simplificación al decir esto pero creo que no afecta demasiado el resultado al que se llega), pero cantidad similar de muestras NO ES IGUAL a cantidad de manos, y eso resulta evidente.
En el caso de VPIP o PFR, casi cada mano que juego es una muestra, ya que en cada mano que juego tengo la opción de decidir si pago o no pago para ver el flop (salvo el caso que me llegue limpeada la mano a BB, pero no se realmente el efecto que tiene eso sobre el VPIP, supongo que esa mano no cuenta pero ese detalle tampoco importa en este análisis) y en todos los casos podré entrar al bote raiseando (salvo que me llegue la mano en situación de allin, y tampoco se como afecta esto al PFR, supongo que tampoco contará esa mano, pero nuevamente ese detalle tampoco importa en este análisis).
En definitiva, si tengo 100 manos de un villano, entonces tengo una cantidad de muestras muy muy cercana a ese valor para el caso de VPIP o PFR.
Que sucede con otras estadísticas?
Pues obviamente la cantidad de manos no representa la cantidad de muestras que se dispone, ya que esas estadísticas se dan bajo determinadas situaciones de juego previas que no ocurren en cada una de las manos en las que participo.
Hablemos de algunas de ellas y vemos que dependen de situaciones totalmente heterogeneas.
- Que se necesita para "alimentar" la estadística CBet de un villano? Pues una mano en la que el villano sea el agresor preflop. Claramente esto indica que esta estadística tendrá a modo general mas muestras en 100 manos para un villano con un PFR cercano a 20 que para un villano con PFR cercano a 10. A modo general podemos decir que la cantidad de manos que se necesitan para considerar como válida esta estadística aumenta a medida que disminuye el PFR del villano.
Vamos a otro tipo de estadísticas, las de steal:
- Que se necesita para "alimentar" la estadística Attempt to Steal from CO de un villano? Pues que la mano le llegue foldeada estando el villano en esa posición.
Ya eso hace que en una mesa FR (9 jugadores), que el villano se encuentre en CO ocurre aproximadamente 11 veces en 100 manos, pero tenemos que agregarle además que la mano le llegue foldeada, por lo cual las muestras válidas que alimenten esta estadística estarán entre 0 y 11, dependiendo justamente de este segundo factor (que basicamente se ve afectado por la agresividad que exista en la mesa).
Mayor efecto tiene la agresividad de la mesa sobre la estadística de Attempt to Steal en BT (o peor aun, en SB) ya que hay un jugador mas que puede raisear o limpear previamente (dos jugadores en el caso de SB).
De esto podríamos concluir que se necesitan mas manos para tener una muestra confiable para el Attempt to Steal en SB que las que se necesitan para una muestra confiable para el Attempt to Steal en BT que a su vez necesita mas manos que las que se necesitarían para tener una muestra confiable para el Attempt to Steal en CO.
Podríamos seguir analizando el resto de las estadísticas, pero creo que ha quedado claro el por qué se necesitan mas mas manos en una estadística que en otra, pero como dije en un primer momento, necesitamos mas manos pero porque queremos disponer de una muestra similar de manos que afecten cada una de las estadísticas.
Aun queda ver que número muestral puede resultar razonable y a partir de ese número muestral podríamos proyectar en función de las restricciones de cada una de las estadísticas (siempre haciendo algunas simplificaciones) la cantidad de manos que en promedio se necesitaría disponer para que la estadística resulte confiable.
(Intentaré hacer alguna estimación del número muestral necesario en el próximo post)
16 años
1.792
16 años
1.792
Debido a una discusión que se armó en otro hilo sobre la validez o no justamente de uno de los datos por el que preguntas (attempt to steal) me he puesto a pensar justamente sobre que cantidad de manos o muestras esas estadísticas estarán mostrando un valor que tenga algún sentido y me he puesto a hacer algunos cálculos y estimaciones.
No tengo esto del todo procesado por lo que mas bien será un brain storming y no un post organizado (seguramente será un ladrillo je).
Como dije esto no está previamente ordenado asi que voy escribiendo a medida que me van surgiendo las ideas.
Supongamos el lanzamiento de una moneda. Asumimos que tanto cara como número tienen la misma probabilidad de ocurrencia (50%).
Si nos preguntamos por ejemlpo cual es la probabilidad de que en 5 lanzamientos consecutivos salga siempre cara, pues la respuesta es sencilla: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Ahora bien, tratemos de involucrar al poker para obtener un resultado similar.
Supongamos un jugador que tenemos en varios miles de manos con un attempt to steal desde SB = 50%. Como se trata de varios miles de manos pues asumimos que el dato se aproxima a la realidad casi sin error.
Ahora bien, que ocurre si queremos calcular la probabilidad de que en una muestra de solamente 5 intentos este jugador intente robar las ciegas todas las veces?
Supongamos por un instante que el jugador decide solamente en función de sus cartas, separa el rango en 50-50 y si le toca una combinación dentro del 50% superior entonces hará el raise y si le toca una combinación dentro del 50% inferior foldeará.
Bajo esa hipótesis la probabilidad de ocurrencia de 5 intentos consecutivos de robo es la misma que en el caso del lanzamiento de la moneda: 0.5*0.5*0.5*0.5*0.5 = 0,03125 -> 3.13%
Pero que diferencia hay entre el poker y el lanzamiento de la moneda?
Pues en mi opinión que un jugador de poker no decide si hacer o no hacer el raise solamente basado en el rango de su mano, mas bien diría que es mas importante el conocimiento de las estadísticas del villano en BB que sus propias cartas.
A que apunto con esto? A que dadas determinadas condiciones (por ejemplo un villano en BB con un elevado fold al attempt to steal desde SB) es mas probable ocurrencias de 5 raises consecutivos en el poker a pesar de que el jugador tenga un 50% de attempt to steal que en el ejemplo del lanzamiento de la moneda. Y obviamente también ocurre a la inversa y es mas probable encontrar secuencias de 5 folds consecutivos en el poker para un jugador con 50% de attempt to steal que nuevamente el ejemplo de la moneda.
Dicho de otra manera, la campana parecería estar mas achatada para el poker que para situaciones que no se ven afectadas por situaciones externas (como es el lanzamiento de la moneda). Esto hace que sea necesario una muestra mayor para darle valor a las estadísticas de la que se necesitaría para verificar por ejemplo la probabilidad de ocurrencia en un lanzamiento (asumiendo que el lanzamiento no se ve afectado por agentes externos).
De todas formas y para simplificar un poco los cálculos, y sobre todo porque no se como mensurar ese achatamiento haré una aproximación al cálculo asumiendo un comportamiento que es ajeno a los componentes externos (básicamente la composición de villanos de la mesa).
(Sigue en próximo post mientras ordeno un poco las ideas)
20 años
21.808
luziphe
(Sigue en próximo post mientras ordeno un poco las ideas)
Te voy a ahorrar un poco de trabajo: Intervalo de confianza.
O bueno, ahora que veo el artículo igual te supone más trabajo, pero vamos, que esto de saber cómo de fiable es un dato basado en cierta muestra ya existe y es de lo más básico del primer curso de estadística de cualquier carrera de números.
nepundTe voy a ahorrar un poco de trabajo: Intervalo de confianza.
O bueno, ahora que veo el artículo igual te supone más trabajo, pero vamos, que esto de saber cómo de fiable es un dato basado en cierta muestra ya existe y es de lo más básico del primer curso de estadística de cualquier carrera de números.
Gracias por el aporte Nepundo, pero no pretendo llegar a un nivel de cálculo tan preciso, solamente tratar de llegar a una aproximación razonable de la cantidad muestral necesaria para que las estadísticas sean válidas (voy al baño y ahora leo con mas detenimiento la refencia que posteaste jeje).
Un saludo.
18 años
7.445
16 años
1.792
Tratando de contestar sobre la pregunta del hilo, en mi opinión todas las estadísticas necesitan una cantidad similar de muestras para ser fiables (estoy haciendo alguna simplificación al decir esto pero creo que no afecta demasiado el resultado al que se llega), pero cantidad similar de muestras NO ES IGUAL a cantidad de manos, y eso resulta evidente.
En el caso de VPIP o PFR, casi cada mano que juego es una muestra, ya que en cada mano que juego tengo la opción de decidir si pago o no pago para ver el flop (salvo el caso que me llegue limpeada la mano a BB, pero no se realmente el efecto que tiene eso sobre el VPIP, supongo que esa mano no cuenta pero ese detalle tampoco importa en este análisis) y en todos los casos podré entrar al bote raiseando (salvo que me llegue la mano en situación de allin, y tampoco se como afecta esto al PFR, supongo que tampoco contará esa mano, pero nuevamente ese detalle tampoco importa en este análisis).
En definitiva, si tengo 100 manos de un villano, entonces tengo una cantidad de muestras muy muy cercana a ese valor para el caso de VPIP o PFR.
Que sucede con otras estadísticas?
Pues obviamente la cantidad de manos no representa la cantidad de muestras que se dispone, ya que esas estadísticas se dan bajo determinadas situaciones de juego previas que no ocurren en cada una de las manos en las que participo.
Hablemos de algunas de ellas y vemos que dependen de situaciones totalmente heterogeneas.
- Que se necesita para "alimentar" la estadística CBet de un villano? Pues una mano en la que el villano sea el agresor preflop. Claramente esto indica que esta estadística tendrá a modo general mas muestras en 100 manos para un villano con un PFR cercano a 20 que para un villano con PFR cercano a 10. A modo general podemos decir que la cantidad de manos que se necesitan para considerar como válida esta estadística aumenta a medida que disminuye el PFR del villano.
Vamos a otro tipo de estadísticas, las de steal:
- Que se necesita para "alimentar" la estadística Attempt to Steal from CO de un villano? Pues que la mano le llegue foldeada estando el villano en esa posición.
Ya eso hace que en una mesa FR (9 jugadores), que el villano se encuentre en CO ocurre aproximadamente 11 veces en 100 manos, pero tenemos que agregarle además que la mano le llegue foldeada, por lo cual las muestras válidas que alimenten esta estadística estarán entre 0 y 11, dependiendo justamente de este segundo factor (que basicamente se ve afectado por la agresividad que exista en la mesa).
Mayor efecto tiene la agresividad de la mesa sobre la estadística de Attempt to Steal en BT (o peor aun, en SB) ya que hay un jugador mas que puede raisear o limpear previamente (dos jugadores en el caso de SB).
De esto podríamos concluir que se necesitan mas manos para tener una muestra confiable para el Attempt to Steal en SB que las que se necesitan para una muestra confiable para el Attempt to Steal en BT que a su vez necesita mas manos que las que se necesitarían para tener una muestra confiable para el Attempt to Steal en CO.
Podríamos seguir analizando el resto de las estadísticas, pero creo que ha quedado claro el por qué se necesitan mas mas manos en una estadística que en otra, pero como dije en un primer momento, necesitamos mas manos pero porque queremos disponer de una muestra similar de manos que afecten cada una de las estadísticas.
Aun queda ver que número muestral puede resultar razonable y a partir de ese número muestral podríamos proyectar en función de las restricciones de cada una de las estadísticas (siempre haciendo algunas simplificaciones) la cantidad de manos que en promedio se necesitaría disponer para que la estadística resulte confiable.
(Intentaré hacer alguna estimación del número muestral necesario en el próximo post)
luzipheen mi opinión todas las estadísticas necesitan una cantidad similar de muestras para ser fiables
No, cuanto más alta sea la magnitud del stat, menos muestras harán falta para que converja. Por ejemplo, el fold to 3bet necesita muchas muestras menos para converger que el 3bet, porque el fold to 3bet se mueve entre valores del 40-90% (por poner un rango), y el 3bet entre valores del 2-9% (por poner un rango también). En la primera un error del 5% es asumible, pero en la segunda un error del 5% invalida totalmente el dato.
Si te pones a calcular intervalos de confianza para cada stat según el número de manos de la muestra te estaremos muy agradecidos, pero es un buen peñazo.
16 años
1.792
16 años
1.792
Tratando de contestar sobre la pregunta del hilo, en mi opinión todas las estadísticas necesitan una cantidad similar de muestras para ser fiables (estoy haciendo alguna simplificación al decir esto pero creo que no afecta demasiado el resultado al que se llega), pero cantidad similar de muestras NO ES IGUAL a cantidad de manos, y eso resulta evidente.
En el caso de VPIP o PFR, casi cada mano que juego es una muestra, ya que en cada mano que juego tengo la opción de decidir si pago o no pago para ver el flop (salvo el caso que me llegue limpeada la mano a BB, pero no se realmente el efecto que tiene eso sobre el VPIP, supongo que esa mano no cuenta pero ese detalle tampoco importa en este análisis) y en todos los casos podré entrar al bote raiseando (salvo que me llegue la mano en situación de allin, y tampoco se como afecta esto al PFR, supongo que tampoco contará esa mano, pero nuevamente ese detalle tampoco importa en este análisis).
En definitiva, si tengo 100 manos de un villano, entonces tengo una cantidad de muestras muy muy cercana a ese valor para el caso de VPIP o PFR.
Que sucede con otras estadísticas?
Pues obviamente la cantidad de manos no representa la cantidad de muestras que se dispone, ya que esas estadísticas se dan bajo determinadas situaciones de juego previas que no ocurren en cada una de las manos en las que participo.
Hablemos de algunas de ellas y vemos que dependen de situaciones totalmente heterogeneas.
- Que se necesita para "alimentar" la estadística CBet de un villano? Pues una mano en la que el villano sea el agresor preflop. Claramente esto indica que esta estadística tendrá a modo general mas muestras en 100 manos para un villano con un PFR cercano a 20 que para un villano con PFR cercano a 10. A modo general podemos decir que la cantidad de manos que se necesitan para considerar como válida esta estadística aumenta a medida que disminuye el PFR del villano.
Vamos a otro tipo de estadísticas, las de steal:
- Que se necesita para "alimentar" la estadística Attempt to Steal from CO de un villano? Pues que la mano le llegue foldeada estando el villano en esa posición.
Ya eso hace que en una mesa FR (9 jugadores), que el villano se encuentre en CO ocurre aproximadamente 11 veces en 100 manos, pero tenemos que agregarle además que la mano le llegue foldeada, por lo cual las muestras válidas que alimenten esta estadística estarán entre 0 y 11, dependiendo justamente de este segundo factor (que basicamente se ve afectado por la agresividad que exista en la mesa).
Mayor efecto tiene la agresividad de la mesa sobre la estadística de Attempt to Steal en BT (o peor aun, en SB) ya que hay un jugador mas que puede raisear o limpear previamente (dos jugadores en el caso de SB).
De esto podríamos concluir que se necesitan mas manos para tener una muestra confiable para el Attempt to Steal en SB que las que se necesitan para una muestra confiable para el Attempt to Steal en BT que a su vez necesita mas manos que las que se necesitarían para tener una muestra confiable para el Attempt to Steal en CO.
Podríamos seguir analizando el resto de las estadísticas, pero creo que ha quedado claro el por qué se necesitan mas mas manos en una estadística que en otra, pero como dije en un primer momento, necesitamos mas manos pero porque queremos disponer de una muestra similar de manos que afecten cada una de las estadísticas.
Aun queda ver que número muestral puede resultar razonable y a partir de ese número muestral podríamos proyectar en función de las restricciones de cada una de las estadísticas (siempre haciendo algunas simplificaciones) la cantidad de manos que en promedio se necesitaría disponer para que la estadística resulte confiable.
(Intentaré hacer alguna estimación del número muestral necesario en el próximo post)
18 años
7.445
luzipheen mi opinión todas las estadísticas necesitan una cantidad similar de muestras para ser fiables
No, cuanto más alta sea la magnitud del stat, menos muestras harán falta para que converja. Por ejemplo, el fold to 3bet necesita muchas muestras menos para converger que el 3bet, porque el fold to 3bet se mueve entre valores del 40-90% (por poner un rango), y el 3bet entre valores del 2-9% (por poner un rango también). En la primera un error del 5% es asumible, pero en la segunda un error del 5% invalida totalmente el dato.
Si te pones a calcular intervalos de confianza para cada stat según el número de manos de la muestra te estaremos muy agradecidos, pero es un buen peñazo.
MokNo, cuanto más alta sea la magnitud del stat, menos muestras harán falta para que converja. Por ejemplo, el fold to 3bet necesita muchas muestras menos para converger que el 3bet, porque el fold to 3bet se mueve entre valores del 40-90% (por poner un rango), y el 3bet entre valores del 2-9% (por poner un rango también). En la primera un error del 5% es asumible, pero en la segunda un error del 5% invalida totalmente el dato.
Si te pones a calcular intervalos de confianza para cada stat según el número de manos de la muestra te estaremos muy agradecidos, pero es un buen peñazo.
Correcto, no había tenido en cuenta la magnitud de la estadística y es otro aspecto importante. Gracias por la aclaración.
No se si llegaré a hacer calculos muy precisos, pero al menos alguna estimación sobre las estadísticas que aqui postearon.
Por cierto Nepundo, he estado leyendo lo que posteaste y que olvidado que estaba en algunos conceptos! Teorema Central del Límite, como 15 años sin oir nada de él jejeje, voy a ver si me re-empapo de algunos conceptos olvidados asi cuando postee los cálculos lo hago con un poco mas de rigor científico que como tenía pensado.
Saludos.
17 años
4.255
[ .]Este hilo puede ser la bomba de divertido :D
[x]Este hilo puede destruir tu cerebro a corto plazo 😒
16 años
1.792
Bien, para el caso de VPIP (aplicable también para PFR) con 1000 manos estamos mas que sobrados, ya que el peor intervalo de confianza lo tendríamos sobre valores de 50%, y el intervalo sería de +- 3.1% (46,9%-53,1%).
Con 200 manos de muestra tenemos el peor intervalo de mano también sobre el 50% (que aqui se de el peor intervalo ocurrirá independientemente de la cantidas de manos de la muestra) y el intervalo sería de +- 6.93% (43.07%-56.97%).
Con 100 manos de muestra el intervalo sería de +- 9.80% (40.20%-59.80%).
De aqui podemos sacar algunas conclusiones, ya que si bien el intervalo de confianza (siempre hablando de un 95% de confianza en todos los cálculos) se hace mas grande a medida que consideramos una muestra menor (lo cual es lógico), en lo que respecta a esta variable y al menos para valores rondando el 50% nuestro juego no se modificará si el villano es realmente un jugador con 50% de VPIP o si realmente es un 40% o un 60%, por lo cual podemos considerar una muestra de 100 manos como razonable para tener una estimación que nos de una idea aproximada del villano al que nos enfrentamos.
Pero que pasa si hablamos de un villano que esté rondando el 10% al 20% de VPIP, es decir donde se concentra la mayor cantidad de villanos?
En ese caso y para 100 manos el peor intervalo de confianza lo tendríamos en el 20%, y el intervalo de confianza sería de +-7,84% (12,16%-27,84%).
En este caso si nos encontramos frente a un problema, ya que no jugaremos de igual forma contra un villano cuyo VPIP es del 13% o 14% que frente a un villano que su VPIP ande rondando el 25%.
Que pasa si la muestra es de 200 manos? Pues la cosa no cambia demasiado y el intervalo es muy similar (no posteo los datos porque no aportan demasiado).
Probemos entonces con una muestra de 500 manos: en ese caso la aproximación mejora un poco, y el intervalo de confianza para el 20% es de +-3.5% (16.5%-23.5%) y si bien no tiene la precisión que muchos pueden pretender si nos da una idea aproximada del villano al que nos estamos enfrentando.
Ya en 1000 manos podemos hablar de un intervalo de confianza de +-2.5% y si somos demasiado puristas, pues 5000 manos nos dan un intervalo de confianza de +-1.11%.
En conclusión (y es mi opinión en función de estos cálculos), creo que 100 manos pueden darnos una idea del rango de VPIP del villano a grandes rasgos, y ser de ayuda, pero deberíamos recién empezar a confiar en su valor para estimar rangos del villano a partir de las 500 a 1000 manos.
17 años
6.442
estoy muy en desacuerdo, pero cada uno con su tema
con 10 manos ya sabes si es un fish o no, 50 o 100 manos sabes a que tiende el jugador, y en 500 manos es muy aproximado
16 años
1.792
17 años
6.442
estoy muy en desacuerdo, pero cada uno con su tema
con 10 manos ya sabes si es un fish o no, 50 o 100 manos sabes a que tiende el jugador, y en 500 manos es muy aproximado
Elbeto8estoy muy en desacuerdo, pero cada uno con su tema
con 10 manos ya sabes si es un fish o no, 50 o 100 manos sabes a que tiende el jugador, y en 500 manos es muy aproximado
Y en que estás en desacuerdo si estás diciendo casi lo mismo que dice el post inmediatamente superior al tuyo? :D
EDIT:
Bueno, no tanto... en 50 manos si se te presenta un jugador con VPIP 20%, pues con una confianza del 95% su valor estará entre 9% y 31%, pero no sabes realmente donde dentro de ese intervalo, y no lo dice luzipher lo dicen las matemáticas.
Saludos.
EDIT 2: Y agrego, si estás en desacuerdo pues te pido que justifiques matematicamente de la misma forma que alguna vez me lo pediste a mi cuando dije que no coincidía con un post tuyo. Aqui si tienes elementos matemáticos para usar, o tu estás en desacuerdo pero tu justificación es "empírica" o viene de "experiencia de juego"?
20 años
21.808
17 años
6.442
estoy muy en desacuerdo, pero cada uno con su tema
con 10 manos ya sabes si es un fish o no, 50 o 100 manos sabes a que tiende el jugador, y en 500 manos es muy aproximado
Elbeto8con 10 manos ya sabes si es un fish o no, 50 o 100 manos sabes a que tiende el jugador, y en 500 manos es muy aproximado
¿Y qué tiene esto de "desacuerdo" con lo que ha puesto luzipher?
Edito: No había visto la respuesta de luzipher... 😁 Y eso, que igual que otras veces sí que estoy en desacuerdo con él ahora no, y creo que tú tampoco.
17 años
6.442
por eso te digo que YO estoy en desacuerdo (y no en otros post que las justificaciones por mi parte son más empíricas cuando matemáticamente tengo el conocimiento para justificarlo) porque lo hago por mi poca experiencia en el juego y considero de que en 100 manos, no puede haber una diferencia de VPIP entre 12 y 28
por supuesto que cada jugador puede cambiar su juego constantemente (tengo gráficas con vpip de 9 y otras de 17 en FR) pero no creo que haya una desviación estándar tan abrupta como marcas en tu post
repito, solo por experiencia, that's all
16 años
1.792
17 años
6.442
por eso te digo que YO estoy en desacuerdo (y no en otros post que las justificaciones por mi parte son más empíricas cuando matemáticamente tengo el conocimiento para justificarlo) porque lo hago por mi poca experiencia en el juego y considero de que en 100 manos, no puede haber una diferencia de VPIP entre 12 y 28
por supuesto que cada jugador puede cambiar su juego constantemente (tengo gráficas con vpip de 9 y otras de 17 en FR) pero no creo que haya una desviación estándar tan abrupta como marcas en tu post
repito, solo por experiencia, that's all
Elbeto8por eso te digo que YO estoy en desacuerdo (y no en otros post que las justificaciones por mi parte son más empíricas cuando matemáticamente tengo el conocimiento para justificarlo) porque lo hago por mi poca experiencia en el juego y considero de que en 100 manos, no puede haber una diferencia de VPIP entre 12 y 28
por supuesto que cada jugador puede cambiar su juego constantemente (tengo gráficas con vpip de 9 y otras de 17 en FR) pero no creo que haya una desviación estándar tan abrupta como marcas en tu post
repito, solo por experiencia, that's all
Bueno, pero aqui estás teniendo un error importante a nivel conceptual, no es que el jugador cambia de juego, la muestra es tan pequeña que el % que se obtiene está afectado justamente por ese valor limitado y puede estar dandote papafritas.
Si tu tiras una moneda 1 millón de veces, seguramente tendrás valores cercanos al 50% de cara y de número. Si la tiras 3 veces tranquilamente puedes tener una secuencia de 3 veces el mismo valor, y no por ello vas a concluir que la moneda está trucada, ya que esto puede ocurrir 1 de cada 4 veces que tires 3 veces una moneda.
En el caso del VPIP ocurre lo mismo, el valor que obtienes en una muestra de 100 manos está afectado por lo reducido de la muestra a tal punto que un villano que se te presente como 20% puede estar realmente en cualquier valor del intervalo 12,16%-27,84% (con una confianza del 95%).
Dices "no creo que haya una desviación estándar tan abrupta como marcas en tu post" a pesar de tener cálculos posteados.
Si digo que 2+2 = 4 me crees pero si posteo algo un poco mas complejo ya no me crees? Como dije anteriormente, no estoy exponiendo una opinión, estoy posteando un cálculo y ahí salvo error en las fórmulas aplicadas no hay otra posibilidad de error (si consideras que no es correcto estás invitado a realizar tus propios cálculos y contrastarlos), no es algo que deba ser valorado desde el "creo o no creo".
Saludos.
17 años
6.442
como te dije anteriormente, es mi opinión a consecuencia de no entender la relación que haces entre confianza, cantidad de manos y desviación estándar
al no entenderlo, ni tampoco conocerte, no voy a fiar en los números que posteas
saludos
16 años
1.792
17 años
6.442
como te dije anteriormente, es mi opinión a consecuencia de no entender la relación que haces entre confianza, cantidad de manos y desviación estándar
al no entenderlo, ni tampoco conocerte, no voy a fiar en los números que posteas
saludos
Elbeto8como te dije anteriormente, es mi opinión a consecuencia de no entender la relación que haces entre confianza, cantidad de manos y desviación estándar
al no entenderlo, ni tampoco conocerte, no voy a fiar en los números que posteas
saludos
Y entonces prefieres postear que estás en total desacuerdo cuando casi casi (salvo lo de las 50 manos) dijiste casi lo mismo que había dicho yo?
Me da mas a pensar que estás en desacuerdo en cualquier cosa que postee, ya no importa si las entiendes o no, que en tratar de entenderlo y contrastarlo...
(Solo para que entiendas lo que estás haciendo, como te sentirías si tu posteas que 3+3 = 6 y viene alguien y te dice: en total desacuerdo, para mi 3+3 no puede dar un número tan grande, es exagerado, no puede dar mas de 4. Y cuando le pides que explique por qué considera eso te contesta que esa es su opinión, que no entiende que significa ese símbolo con los palitos cruzados (+), pero que le sigue pareciendo que 6 es mucho porque no te conoce y no tiene por qué confiar en vos.)
Bueno, dejando esto de lado, intento seguir con otra de las stats.
En realidad son 3, pero podriamos tratarlas en el mismo grupo: las stats de steal.
El problema que presentan estas stats es lo que indiqué en uno de los primeros posts, y es que las veces que estas stats se ven afectadas está bastante distante de la cantidad de manos jugadas.
El mejor escenario es que la relación sea 1/9 en FR, pero esto obviamente no es sostenible en el tiempo y solo ocurriría en mesas con jugadores/flop casi ridiculo.
De todas formas y para facilidad del cálculo podemos considerar que cada 10 manos tenemos una muestra válida para estas stats, sabiendo que estamos siendo generosos en este aspecto (para mas precisión podriamos consultar una BD para ver una relación mas precisa en función de las mesas en las que acostumbramos jugar).
Teniendo en cuenta que la magnitud de estas variables rondará valores similares a los del VPIP (tal vez un poco mas elevados), entonces podemos usar la aproximación que se hizo para estimar intervalos de confianza en ese caso, solo que debemos multiplicar por el coeficiente que consideremos (10 para simplificar como dijimos) la cantidad de manos necesarias.
En este caso nos ahorramos los cálculos, ya que los tenemos realizados para el VPIP y lo que podemos concluir es que si 50 manos eran muy pocas para tener una precisión aceptable para el VPIP, entonces 500 manos serán pocas para el caso del steal.
Recién a partir de las 1000 manos tendremos una idea de tendencia de dichas stats, pero recién a partir de las 10.000 manos podemos asumir un error que rondará un 3% (siempre con una confianza del 95%).
Que sucede en una muestra de 100 manos, es decir, que en el mejor escenario dispone de una decena de valores muestrales para esta estadística?
Pues que si la stat nos indica un 50%, el intervalo de confianza es tan grosero (19%-81%) que usar ese dato es completamente inutil.
Lo razonable cuando se dispone de una centena de manos para estas stats, es ni siquiera tener en cuenta el valor que muestra el HUD y posicionar al villano en función de sus valores de VPIP/PFR, asumiendo para estas stats valores estandar.
Si el villano que estamos enfrentando es un villano con valores de VPIP y PFR similares, y con valores en el rango de 12 a 25 para esa muestra, entonces es mas razonable asumir que su valor de attempt to steal estará entre el 25% y el 50% que basarnos en lo que nos indique el HUD, que como vimos puede ser cualquier cosa.
La próxima stat que intentaré analizar es alguna (como indicó Moke) que tenga valores bajos y por lo tanto requieran una mayor cantidad de muestras para llegar a un valor que resulte confiable.
17 años
6.442
luzipher, tenes un gran problema de paranoia
cuando posteo, no suelo ver ni a quien quoteo ni con quien me contradigo, a excepcion de personas que les tengo un respeto especial al considerar que están a años luz de mis conocimientos y uno siempre debe sacarle el jugo a cada una de sus palabras, ya todos sabemos quienes son y no voy a nombrar a nadie
si queres pensar que tengo un problema con vos, estás muy equivocado, los cálculos que haces me parece que no son tan empíricos como una simple suma, pero si te esmerás en responder con ironía, allá vos, suerte con tu investigación
saludos
pd. me autocito para aclara que estoy en desacuerdo en "considero de que en 100 manos, no puede haber una diferencia de VPIP entre 12 y 28"
16 años
1.792
17 años
6.442
luzipher, tenes un gran problema de paranoia
cuando posteo, no suelo ver ni a quien quoteo ni con quien me contradigo, a excepcion de personas que les tengo un respeto especial al considerar que están a años luz de mis conocimientos y uno siempre debe sacarle el jugo a cada una de sus palabras, ya todos sabemos quienes son y no voy a nombrar a nadie
si queres pensar que tengo un problema con vos, estás muy equivocado, los cálculos que haces me parece que no son tan empíricos como una simple suma, pero si te esmerás en responder con ironía, allá vos, suerte con tu investigación
saludos
pd. me autocito para aclara que estoy en desacuerdo en "considero de que en 100 manos, no puede haber una diferencia de VPIP entre 12 y 28"
Elbeto8luzipher, tenes un gran problema de paranoia
cuando posteo, no suelo ver ni a quien quoteo ni con quien me contradigo, a excepcion de personas que les tengo un respeto especial al considerar que están a años luz de mis conocimientos y uno siempre debe sacarle el jugo a cada una de sus palabras, ya todos sabemos quienes son y no voy a nombrar a nadie
si queres pensar que tengo un problema con vos, estás muy equivocado, los cálculos que haces me parece que no son tan empíricos como una simple suma, pero si te esmerás en responder con ironía, allá vos, suerte con tu investigación
saludos
No respondí con ironía, fui directo y no hay paranoia sino es la unica explicación que le encuentro a la respuesta de alguien que dice que está en completo desacuerdo con algo que se postea, que dice no entenderlo y sin embargo además está diciendo casi lo mismo que tu dijiste, revisa lo que posteaste y los argumentos que diste y verás de que hablo.
No lo entiendes, estás en completo desacuerdo pero casi decimos lo mismo! De locos realmente...
Revisa también que entiendes por "empírico" porque lo estás aplicando mal, la suma por mas que sea "sencilla" no es un concepto empírico y está sostenido por unos cuantos teoremas (y lo digo sin ironía, realmente lo estás aplicando mal).
Y tampoco pretendo seguir con temas que no son los del hilo en cuestión, si quieres discutir algo mas que no esté relacionado al hilo te invito a escribirme un PM y la seguimos por allí.
Saludos.
16 años
1.792
17 años
6.442
luzipher, tenes un gran problema de paranoia
cuando posteo, no suelo ver ni a quien quoteo ni con quien me contradigo, a excepcion de personas que les tengo un respeto especial al considerar que están a años luz de mis conocimientos y uno siempre debe sacarle el jugo a cada una de sus palabras, ya todos sabemos quienes son y no voy a nombrar a nadie
si queres pensar que tengo un problema con vos, estás muy equivocado, los cálculos que haces me parece que no son tan empíricos como una simple suma, pero si te esmerás en responder con ironía, allá vos, suerte con tu investigación
saludos
pd. me autocito para aclara que estoy en desacuerdo en "considero de que en 100 manos, no puede haber una diferencia de VPIP entre 12 y 28"
Elbeto8
pd. me autocito para aclara que estoy en desacuerdo en "considero de que en 100 manos, no puede haber una diferencia de VPIP entre 12 y 28"
No había visto este agregado.
Te doy argumentos del por qué:

Calcula el intervalo para n=100 (la cantidad de manos) y p(con techito) del 20% como en el ejemplo que postee y verás cuanto te da el intervalo de confianza.
Esa fórmula es para calcular el intervalo de confianza de una proporción.
En realidad para valores menores o iguales a 100 (y mayores a 30) deberías aplicar esta otra:
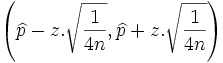
Pero en este caso te dará un intervalo aún mayor (10.20-29.80) (z=1.96)
Saludos.
16 años
1.792
Vamos por la siguiente, el 3bet y tomemos el aporte de Moke:
MokNo, cuanto más alta sea la magnitud del stat, menos muestras harán falta para que converja. Por ejemplo, el fold to 3bet necesita muchas muestras menos para converger que el 3bet, porque el fold to 3bet se mueve entre valores del 40-90% (por poner un rango), y el 3bet entre valores del 2-9% (por poner un rango también). En la primera un error del 5% es asumible, pero en la segunda un error del 5% invalida totalmente el dato.
Si te pones a calcular intervalos de confianza para cada stat según el número de manos de la muestra te estaremos muy agradecidos, pero es un buen peñazo.
Si asumimos la stat dentro de ese rango (lo cual resulta razonable), entonces no deberíamos permitirnos un error mayor al 0,5%.
Para ello podríamos calcular el peor escenario, que se daría en el 9%, y asumiendo ese rango de error.
Si aplicamos esta fórmula:
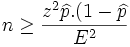
para determinar el tamaño muestral que necesitamos.
Calculando para:
p(con techito) = 0.09
E = 0.005
z = 1.96
Entonces llegamos a que necesitamos un tamaño muestral n>=12585
Como vimos el tamaño muestral no es igual que la cantidad de manos para las stats que no sean VPIP o PFR.
Que sucede en el caso del 3bet? Pues tiene que existir un raiser previo y llegarnos en esas condiciones la mano.
Esto ocurre con cierta frecuencia, sobre todo a medida que nuestra posición está mas cercana al botón o ciegas.
Nuevamente, podríamos ver nuestra base de datos y verificar en nuestras estadísticas cuantas veces estamos en situación de 3bet en el total de manos que tenemos registradas en las mesas donde acostumbramos jugar para obtener un coeficiente por el cual multiplicar el tamaño muestral al que llegamos.
Si consideramos un valor para ese coeficiente de 3, entonces estaríamos necesitando unas 37K a 40K para tener el 3bet con un error que no sea superior al 0,5%.
Parece mucho...
Si somos un poco mas tolerantes, y aceptamos el valor con un margen de error de 1%, entonces rehaciendo los cálculos para el 9% (extremo superior del intervalo) nos da que necesitamos un tamaño muestral mas razonable n>=3146
Por otro lado, ese espacio muestral nos permite tener un error en el extremo inferior del intervalo (2%) que no supere el 0,5%, y es en ese extremo donde necesitamos mas precisión, ya que en ese extremo no deberíamos tolerar un error del 1% (no es lo mismo 1% de 3bet que 3%, está mas que claro).
Como dije, si hacemos los calculos para el extremo inferior y tolerando un error de 0.5% nos da un espacio muestral n>=3012.
Entonces podemos considerar que a partir de las 7000 a 10000 manos tenemos un valor razonable de aproximación al 3bet.
Si toleramos un error que sea del 1.5% para el extremo superior (9%) y del 0.75% en el extremo inferior (2%), entonces podemos tener una aproximación al valor de 3bet en una muestra cercana a las 4000 manos.
En 1000 manos podemos decir que el error es tan grande (por ej: 9%+-3% o 2%+-1.5%) que el valor no es fiable como para jugar con rangos de 3bet del villano, solamente nos estaría dando una aproximación del estilo de juego, pero no lo suficientemente adecuada como para valorar el equity de nuestra mano frente a su rango (salvo que de todas formas tengamos un equity favorable contra el peor escenario, eso está claro).
Saludos.
19 años
2.662
16 años
1.792
Vamos por la siguiente, el 3bet y tomemos el aporte de Moke:
MokNo, cuanto más alta sea la magnitud del stat, menos muestras harán falta para que converja. Por ejemplo, el fold to 3bet necesita muchas muestras menos para converger que el 3bet, porque el fold to 3bet se mueve entre valores del 40-90% (por poner un rango), y el 3bet entre valores del 2-9% (por poner un rango también). En la primera un error del 5% es asumible, pero en la segunda un error del 5% invalida totalmente el dato.
Si te pones a calcular intervalos de confianza para cada stat según el número de manos de la muestra te estaremos muy agradecidos, pero es un buen peñazo.
Si asumimos la stat dentro de ese rango (lo cual resulta razonable), entonces no deberíamos permitirnos un error mayor al 0,5%.
Para ello podríamos calcular el peor escenario, que se daría en el 9%, y asumiendo ese rango de error.
Si aplicamos esta fórmula:
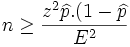
para determinar el tamaño muestral que necesitamos.
Calculando para:
p(con techito) = 0.09
E = 0.005
z = 1.96
Entonces llegamos a que necesitamos un tamaño muestral n>=12585
Como vimos el tamaño muestral no es igual que la cantidad de manos para las stats que no sean VPIP o PFR.
Que sucede en el caso del 3bet? Pues tiene que existir un raiser previo y llegarnos en esas condiciones la mano.
Esto ocurre con cierta frecuencia, sobre todo a medida que nuestra posición está mas cercana al botón o ciegas.
Nuevamente, podríamos ver nuestra base de datos y verificar en nuestras estadísticas cuantas veces estamos en situación de 3bet en el total de manos que tenemos registradas en las mesas donde acostumbramos jugar para obtener un coeficiente por el cual multiplicar el tamaño muestral al que llegamos.
Si consideramos un valor para ese coeficiente de 3, entonces estaríamos necesitando unas 37K a 40K para tener el 3bet con un error que no sea superior al 0,5%.
Parece mucho...
Si somos un poco mas tolerantes, y aceptamos el valor con un margen de error de 1%, entonces rehaciendo los cálculos para el 9% (extremo superior del intervalo) nos da que necesitamos un tamaño muestral mas razonable n>=3146
Por otro lado, ese espacio muestral nos permite tener un error en el extremo inferior del intervalo (2%) que no supere el 0,5%, y es en ese extremo donde necesitamos mas precisión, ya que en ese extremo no deberíamos tolerar un error del 1% (no es lo mismo 1% de 3bet que 3%, está mas que claro).
Como dije, si hacemos los calculos para el extremo inferior y tolerando un error de 0.5% nos da un espacio muestral n>=3012.
Entonces podemos considerar que a partir de las 7000 a 10000 manos tenemos un valor razonable de aproximación al 3bet.
Si toleramos un error que sea del 1.5% para el extremo superior (9%) y del 0.75% en el extremo inferior (2%), entonces podemos tener una aproximación al valor de 3bet en una muestra cercana a las 4000 manos.
En 1000 manos podemos decir que el error es tan grande (por ej: 9%+-3% o 2%+-1.5%) que el valor no es fiable como para jugar con rangos de 3bet del villano, solamente nos estaría dando una aproximación del estilo de juego, pero no lo suficientemente adecuada como para valorar el equity de nuestra mano frente a su rango (salvo que de todas formas tengamos un equity favorable contra el peor escenario, eso está claro).
Saludos.
luziphe
Entonces podemos considerar que a partir de las 7000 a 10000 manos tenemos un valor razonable de aproximación al 3bet.
Entonces me imagino que el fold 4 bet nunca lo podrmos utilizar bien ya que necesitariamos miles y miles de manos... cdo tengamos esa cantiddad el rival ya puede haber cambiado su forma de jugar....
16 años
1.792
16 años
1.792
Vamos por la siguiente, el 3bet y tomemos el aporte de Moke:
MokNo, cuanto más alta sea la magnitud del stat, menos muestras harán falta para que converja. Por ejemplo, el fold to 3bet necesita muchas muestras menos para converger que el 3bet, porque el fold to 3bet se mueve entre valores del 40-90% (por poner un rango), y el 3bet entre valores del 2-9% (por poner un rango también). En la primera un error del 5% es asumible, pero en la segunda un error del 5% invalida totalmente el dato.
Si te pones a calcular intervalos de confianza para cada stat según el número de manos de la muestra te estaremos muy agradecidos, pero es un buen peñazo.
Si asumimos la stat dentro de ese rango (lo cual resulta razonable), entonces no deberíamos permitirnos un error mayor al 0,5%.
Para ello podríamos calcular el peor escenario, que se daría en el 9%, y asumiendo ese rango de error.
Si aplicamos esta fórmula:
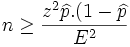
para determinar el tamaño muestral que necesitamos.
Calculando para:
p(con techito) = 0.09
E = 0.005
z = 1.96
Entonces llegamos a que necesitamos un tamaño muestral n>=12585
Como vimos el tamaño muestral no es igual que la cantidad de manos para las stats que no sean VPIP o PFR.
Que sucede en el caso del 3bet? Pues tiene que existir un raiser previo y llegarnos en esas condiciones la mano.
Esto ocurre con cierta frecuencia, sobre todo a medida que nuestra posición está mas cercana al botón o ciegas.
Nuevamente, podríamos ver nuestra base de datos y verificar en nuestras estadísticas cuantas veces estamos en situación de 3bet en el total de manos que tenemos registradas en las mesas donde acostumbramos jugar para obtener un coeficiente por el cual multiplicar el tamaño muestral al que llegamos.
Si consideramos un valor para ese coeficiente de 3, entonces estaríamos necesitando unas 37K a 40K para tener el 3bet con un error que no sea superior al 0,5%.
Parece mucho...
Si somos un poco mas tolerantes, y aceptamos el valor con un margen de error de 1%, entonces rehaciendo los cálculos para el 9% (extremo superior del intervalo) nos da que necesitamos un tamaño muestral mas razonable n>=3146
Por otro lado, ese espacio muestral nos permite tener un error en el extremo inferior del intervalo (2%) que no supere el 0,5%, y es en ese extremo donde necesitamos mas precisión, ya que en ese extremo no deberíamos tolerar un error del 1% (no es lo mismo 1% de 3bet que 3%, está mas que claro).
Como dije, si hacemos los calculos para el extremo inferior y tolerando un error de 0.5% nos da un espacio muestral n>=3012.
Entonces podemos considerar que a partir de las 7000 a 10000 manos tenemos un valor razonable de aproximación al 3bet.
Si toleramos un error que sea del 1.5% para el extremo superior (9%) y del 0.75% en el extremo inferior (2%), entonces podemos tener una aproximación al valor de 3bet en una muestra cercana a las 4000 manos.
En 1000 manos podemos decir que el error es tan grande (por ej: 9%+-3% o 2%+-1.5%) que el valor no es fiable como para jugar con rangos de 3bet del villano, solamente nos estaría dando una aproximación del estilo de juego, pero no lo suficientemente adecuada como para valorar el equity de nuestra mano frente a su rango (salvo que de todas formas tengamos un equity favorable contra el peor escenario, eso está claro).
Saludos.
19 años
2.662
luziphe
Entonces podemos considerar que a partir de las 7000 a 10000 manos tenemos un valor razonable de aproximación al 3bet.
Entonces me imagino que el fold 4 bet nunca lo podrmos utilizar bien ya que necesitariamos miles y miles de manos... cdo tengamos esa cantiddad el rival ya puede haber cambiado su forma de jugar....
EduargentinEntonces me imagino que el fold 4 bet nunca lo podrmos utilizar bien ya que necesitariamos miles y miles de manos... cdo tengamos esa cantiddad el rival ya puede haber cambiado su forma de jugar....
Para que te hagas una idea yo tengo 110 manos en las que me he enfrentado a un 4bet en las ultimas 98K manos.
Como hemos visto hasta ahora recién a partir de un muestreo de 100 podemos llegar a tener una idea, y recién una aproximación razonable a partir de las 500, por lo que necesitaríamos 500K manos para tener una aproximación válida (minimo 100K para tener una cierta idea y eso teniendo en cuenta la relación que encuentro entre manos en las que me enfrento a un 4bet en función del total de manos en mi realidad particular)
Saludos.
16 años
1.792
Había posteado el coeficiente 3 para el caso de la stat 3bet estando en el trabajo, y haciendo una aproximación a ojo de las veces que nos enfrentabamos a una situación en la que podíamos 3betear sobre el total de manos, y la verdad es que no estuvo muy alejado de lo que obtengo en mi base de datos.
98702 manos de las cuales estuve en posición de realizar un 3bet 30751.
98702/30751 = 3.21 para el coeficiente, por lo cual las estimaciones realizadas para esa stat son bastante precisas.
AGREGO:
En cuanto a la stat de steal, en 98702 manos solamente en 5518 me llegó la mano foldeada estando en CO, 4063 veces estando en BT y solo 2579 veces estando en SB.
Esto muestra que el coeficiente 10 que usé era demasiado generoso y debe usarse:
- aprox. 20 para el caso del Attempt to steal from CO
- aprox. 25 para el caso del Attempt to steal from BT
- aprox. 40 para el caso del Attempt to steal from SB
Al menos en el sitio/mesas que acostumbro jugar yo (PS, NL100 FR, las mesas con el mayor valor de Jugadores/Flop que encuentro con pocos o sin SS)
Saludos.
18 años
7.445
Qué malos recuerdos de la facultad me han traído esas fórmulas:P Sinceramente no me apetece nada ponerme a comprobar las cuentas, pero echando un ojo por encima tiene buena pinta y los resultados a priori me parecen bastante razonables. Un intervalo de confianza del 95% quiere decir que 1 de cada 20 veces caerá un valor fuera de él. Os parece muy exagerado que 1 de cada 20 veces un villano con un VPIP de 20% nos aparezca como 28% en una muestra de 100 manos? A mi me parece muy normal. Lo mismo me pasa con el resto de los stats.
De cualquier forma, que se necesiten muestras de manos muy grandes para tener un intervalo de confianza del 95% no quiere decir que los datos no se puedan usar hasta tener muestras tan grandes. Si tengo A9s y sé que el intervalo de confianza del att to steal de un villano es de 30%-90%, me la pela, le voy a 3betear a cualquier valor de ese intervalo. Si el intervalo es del 20-90% y no me hace gracia 3betearle A9s a un tipo con 20% de steal, me la pela igual, porque más del 90% de las veces (así a ojo) el 3bet será correcto (los valores de los extremos de la campana son mucho menos probables que los del centro), y asumo el error que pueda tener el dato. Es mucho más delicado saber cuánto error puedo asumir y cuánto me cuesta asumir un dato erróneo, pero que el att to steal en 200 manos tenga un intervalo de confianza muy amplio no quiere decir que no lo pueda utilizar (con cuidado).
Aparte de esto, algunos de los jugadores (sea la proporción que sea) apuestan o dejan de apostar en función de la situación y del rival, no sólo de las cartas. Esto hace que la varianza de los datos baje drásticamente al no depender directamente de lo que tengan en la mano.
En conclusión, tampoco hay que asustarse tanto porque salgan unas muestras tan grandes. Entre que nuestros rivales juegan en mayor o menor medida respecto a la situación y no a las cartas, que los valores se concentran en el centro del intervalo de confianza y no en los extremos, y que podemos asumir cierta cantidad de error, podemos utilizar muestras sensiblemente más pequeñas siendo conscientes de que estamos asumiendo ese error.
De cualquier forma, la inmensa mayoría de la gente tiende a fiarse de muestras pequeñísimas de manos, y todos los días vemos gente teniendo en cuenta la cbet en el turn, la agg% en el river, el 4bet, el bet ante missed cbet, el fold cbet en botes 3beteados y muchos más stats en muestras 1k o 2k manos, cuando igual sólo hubo 6 o 9 situaciones de esas y la fiabilidad del dato es de risa. Esa debería ser la moraleja final.
16 años
1.792
De acuerdo moke en lo que dices, y agregaría (ya lo dije y lo remarco) que es mejor fiarse de un stat promedio o estimado de una media poblacional conocida de villanos que creer en un número en una muestra de risa.
En el ejemplo del A9, y cuando consideras que estás haciendo un 3bet correcto debido a que los valores de los extremos de la campana son mucho menos probables que los del centro, si el intervalo es 20%-90%, entonces justamente estamos en una situación muestral de risa. Yo ahi me decanto por hacer el 3bet por valor frente a un rival que tenga valores de VPIP/PFR razonables, ya que asumo que la gran mayoría de esos villanos tendrá el attempt to steal from SB lo suficientemente grande como para que mi 3bet sea por valor. Y lo digo porque enfrentado a una realidad exactamente opuesta, en la que el dato que veo es por ejemplo 12.5% (o 16.7%) siempre en unas 100 manos, pues también con A9 metería el 3bet por valor, ya que considero que esa muestra es de risa y no me fio absolutamente de ella, y prefiero arriesgarme basado en un valor muestral promedio de un villano tipo que en un dato particular que está muy afectado por la muestra pequeña.
Otra cosa que muchas veces no son tenidas en cuenta al momento de analizar las stats es que justamente dependen o se ven afectadas por la forma en que te está viendo el villano a ti.
Si el villano te ve con un fold elevado al attempt to steal (por nombrar una), entonces su rango de steal será mayor seguramente que el valor que puedas estimar de su estadística de attempt to steal desde CO (por nombrar alguna) aunque dispongas de una muestra elevada, y esto ocurre justamente porque tu tal vez seas un villano que el ve como explotable.
Justamente lo contrario ocurriría si tu defiendes tus ciegas con uñas y dientes. Si el villano sabe analizar stats entonces su rango de steal será mucho mas reducido que el que puedas estimar a partir de la stat que tu ves de él, y ahi puedes creer que estás metiendo un 3bet adecuado cuando seguramente te encuentres con un rango mucho mas reducido de OR y la consecuente 4bet.
Igual esto ya escapa al alcance que pretendía de esto que era la legitimidad a nivel estadístico de las distintas stats con las que en general nos manejamos.
Muy buena la moraleja, 100% de acuerdo.
Saludos.
18 años
7.445
Hombre, aunque el intervalo de confianza sea amplísimo, algún significado podemos extraer de él. Por ejemplo, en la del 20-90%, al menos sabemos que no es un nitazo con menos de un 20% de steal, y también sabemos que lo más probable es que tenga un steal elevado, más alto que el de la media del nivel.
La imagen que tiene el villano de ti ya es otro tema. De hecho un stat que yo hecho muchíiiiiisimo de menos es las veces que un villano hace un movimiento exclusivamente contra ti. Tanto lo hecho de menos que llevo la cuenta de algunos manualmente en las notas, como el número de veces que me reroba preflop, las raises a mis cbets postflop, etc. Vale que voy a necesitar una muestra enorme de manos, pero en niveles medios hay bastantes regulares de los que vas a tener muestras mayores a 5k o incluso a 10k manos, y ahí ya pueden tener fiabilidad.
16 años
1.792
18 años
7.445
Hombre, aunque el intervalo de confianza sea amplísimo, algún significado podemos extraer de él. Por ejemplo, en la del 20-90%, al menos sabemos que no es un nitazo con menos de un 20% de steal, y también sabemos que lo más probable es que tenga un steal elevado, más alto que el de la media del nivel.
La imagen que tiene el villano de ti ya es otro tema. De hecho un stat que yo hecho muchíiiiiisimo de menos es las veces que un villano hace un movimiento exclusivamente contra ti. Tanto lo hecho de menos que llevo la cuenta de algunos manualmente en las notas, como el número de veces que me reroba preflop, las raises a mis cbets postflop, etc. Vale que voy a necesitar una muestra enorme de manos, pero en niveles medios hay bastantes regulares de los que vas a tener muestras mayores a 5k o incluso a 10k manos, y ahí ya pueden tener fiabilidad.
MokHombre, aunque el intervalo de confianza sea amplísimo, algún significado podemos extraer de él. Por ejemplo, en la del 20-90%, al menos sabemos que no es un nitazo con menos de un 20% de steal, y también sabemos que lo más probable es que tenga un steal elevado, más alto que el de la media del nivel.
Para poder concluir eso pues necesitamos al menos una muestra de 10 situaciones, las cuales ocurrirán entre las 200 a 400 manos en promedio.
Si disponemos de una cantidad inferior de muestras, por ejemplo 6 o 7, entonces el intervalo de confianza es absolutamente ridiculo.
Lo que no veo tan claro es que podamos concluir tan libremente que su steal esté por encima de la media en el nivel con una muestra tan pequeña.
Si disponemos de 10 muestras, pues en el HUD veremos 60, o veremos 50, o veremos 40 (por nombrar algunos de los posibles datos), y no veremos ningún valor intermedio. Ver un 50% en una muestra de 10 no me puede de ninguna manera permitir concluir que el villano tendrá un attempt to steal >35%. Podré descartar tal vez un 25 a 20 y un 85 a 90 si tenemos el intervalo de confianza en 20-90, pero no podemos ir mas allá de eso y asegurar que su valor no termine siendo cualquier otro dentro del intervalo en cuestión. Si disponemos de menos de 10 muestras ya ni siquiera tiene sientido plantearse esta situación, ya que el intervalo de confianza termina siendo practicamente todos los posibles valores.
Sigo pensando que en una muestra reducida es mejor apuntar al valor de VPIP/PFR que al valor sin sentido que pueda verse en una muestra de risa.
Si me enfrento a un villano que en 100 manos es 7/4 y su attempt to steal aparece en 50% foldearé seguramente mi A9, sin embargo frente a un 20/20 en la misma cantidad de manos que presente un attempt to steal en 50% optaré por el 3bet, pero no justamente por el valor de la stat sino por el apoyo de las otras stats que tienen un poco mas de valor estadístico en una muestra de 100 manos y me dan una idea un poco mas aproximada de lo que el villano finalmente puede llegar a ser en realidad. Me puedo equivocar en cualquiera de los dos casos, pero en mi opinión tendré mas precisión en la decisión si me baso en stats que ya estén aproximando al valor real en función de la muestra que tengo y proyectar otras stats a partir de las 1eras que ya tienen cierta validez, que usar valores de stats en muestras de risa.
Saludos.
19 años
3.550
Para que una hipotesis sea considerada como cierta, es un standard probarla con un 95% de confianza, no menos.
19 años
2.662
LUzipher podrias hacer un resumen tipo, para vpip X manos, para att steal X manos y asi? gracias, lindo laburito te pegaste
19 años
2.662
En torneos el único dato confiable seria VPIP y PFR, no?
16 años
1.792
Edu, luego hago un resumen, pero es bastante sencillo.
Sobre torneos el problema que existe es que los villanos obviamente van modificando su estilo en función de la etapa del torneo y su stack relativo (obviamente hay muchos otros factores que afectan la forma de juego: estructura de premios, de ciegas, etc).
De todas formas considero que hay alguna otra stat que puede tener un grado importante de confiabilidad, siempre teniendo en cuenta las observaciones anteriores, como por ejemplo el cbet.
En lo que respecta al steal, si a la cantidad de manos necesarias para que la stat sea confiable le agregas la dificultad de separar la etapa del torneo donde el dato fue obtenido entonces se hace practicamente inutil. Solamente usaría ese tipo de stats para tener una idea aproximada del estilo de juego del villano, pero nunca proyectaría un rango en función del dato que me muestra el programa.
Por ejemplo si recordamos aquella mano en el SCOOP, JTo de Raul Mestre y compañía, veremos que ellos consideraban que el OR del villano en SB era de practicamente el 100%, pero ese dato no salía de una herramienta estadística, lo mismo ocurría con el rango de 4bet que estimaban. En mi opinión es mejor fiarse del conocimiento que se tenga del villano en efrentamientos previos (en ese caso creo que era Thalai el que lo conocía) y la proyección que se pueda hacer del mismo a la situación actual del torneo que guiarse por estadísticas que probablemente estén basadas en una cantidad de manos insuficiente y afectadas además por los factores que indiqué previamente. Creo que si eres lo suficientemente observador sabrás mas de un villano a través de su juego en 2 o 3 orbitas que usando estadísticas poco confiables.
Saludos.
19 años
2.662
16 años
1.792
Edu, luego hago un resumen, pero es bastante sencillo.
Sobre torneos el problema que existe es que los villanos obviamente van modificando su estilo en función de la etapa del torneo y su stack relativo (obviamente hay muchos otros factores que afectan la forma de juego: estructura de premios, de ciegas, etc).
De todas formas considero que hay alguna otra stat que puede tener un grado importante de confiabilidad, siempre teniendo en cuenta las observaciones anteriores, como por ejemplo el cbet.
En lo que respecta al steal, si a la cantidad de manos necesarias para que la stat sea confiable le agregas la dificultad de separar la etapa del torneo donde el dato fue obtenido entonces se hace practicamente inutil. Solamente usaría ese tipo de stats para tener una idea aproximada del estilo de juego del villano, pero nunca proyectaría un rango en función del dato que me muestra el programa.
Por ejemplo si recordamos aquella mano en el SCOOP, JTo de Raul Mestre y compañía, veremos que ellos consideraban que el OR del villano en SB era de practicamente el 100%, pero ese dato no salía de una herramienta estadística, lo mismo ocurría con el rango de 4bet que estimaban. En mi opinión es mejor fiarse del conocimiento que se tenga del villano en efrentamientos previos (en ese caso creo que era Thalai el que lo conocía) y la proyección que se pueda hacer del mismo a la situación actual del torneo que guiarse por estadísticas que probablemente estén basadas en una cantidad de manos insuficiente y afectadas además por los factores que indiqué previamente. Creo que si eres lo suficientemente observador sabrás mas de un villano a través de su juego en 2 o 3 orbitas que usando estadísticas poco confiables.
Saludos.
luzipheEdu, luego hago un resumen, pero es bastante sencillo.
Sobre torneos el problema que existe es que los villanos obviamente van modificando su estilo en función de la etapa del torneo y su stack relativo (obviamente hay muchos otros factores que afectan la forma de juego: estructura de premios, de ciegas, etc).
De todas formas considero que hay alguna otra stat que puede tener un grado importante de confiabilidad, siempre teniendo en cuenta las observaciones anteriores, como por ejemplo el cbet.
En lo que respecta al steal, si a la cantidad de manos necesarias para que la stat sea confiable le agregas la dificultad de separar la etapa del torneo donde el dato fue obtenido entonces se hace practicamente inutil. Solamente usaría ese tipo de stats para tener una idea aproximada del estilo de juego del villano, pero nunca proyectaría un rango en función del dato que me muestra el programa.
Por ejemplo si recordamos aquella mano en el SCOOP, JTo de Raul Mestre y compañía, veremos que ellos consideraban que el OR del villano en SB era de practicamente el 100%, pero ese dato no salía de una herramienta estadística, lo mismo ocurría con el rango de 4bet que estimaban. En mi opinión es mejor fiarse del conocimiento que se tenga del villano en efrentamientos previos (en ese caso creo que era Thalai el que lo conocía) y la proyección que se pueda hacer del mismo a la situación actual del torneo que guiarse por estadísticas que probablemente estén basadas en una cantidad de manos insuficiente y afectadas además por los factores que indiqué previamente. Creo que si eres lo suficientemente observador sabrás mas de un villano a través de su juego en 2 o 3 orbitas que usando estadísticas poco confiables.
Saludos.
Al final no hiciste el resumen :P je
16 años
1.792
jejeje, esta noche si tengo un tiempito o mañana hago el resumen.
Saludos.
17 años
3.872
Luzipher, buenas reflexiones. Creo que es muy útil que todos pensemos en la fiablidad de las estadísticas que utilizamos. Pero la verdad es que cuesta mucho hablar de estos temas sin liar más de lo que se aclara.
Lo que no veo es la necesidad de relacionar las manos totales de un jugador con la fiablidad de una estadística concreta. Para saber si esa estadística es fiable deberíamos fijarnos en las manos que tenemos de ella. En el PT por ejemplo, si pones el puntero del ratón encima de una te dice sobre cuantas manos está hecha. Esa en la "n" que deberíamos fijarnos.
Usando las probabilidades de muestreo, basadas en las formulas que has puesto, sabemos que tendremos un intervalo del 5% cuando (por ejemplo para el VP$IP):
- Para un VP$IP del 50%, el intervalo será de 45%-55% a partir de una muestra de 400.
- Para un VP$IP del 20%, el intervalo será de 15%-25% a partir de una muestra de 235.
-Para un VP$IP del 80%, el intervalo será de 75%-85% a partir de una muestra de 235 (un porcentaje de (x) y de (1-x) generan el mismo intervalo de confianza).
- Para un VP$IP del 10%, el intervalo será de 5%-15% a partir de una muestra de 138.
Hay que tener en cuenta que dentro del intervalo generado no todos los puntos tienen la misma probabilidad de darse. Así, para el primer caso es mucho más probable que el VP$IP sea realmente del 50% que del 45% (normalidad en los intervalos).
Tambien hay que pensar que este es el intervalo para evaluar 1 estadística de 1 persona y que en el largo plazo evaluaremos miles de estadísticas de miles de personas. Por tanto las veces que nos equivoquemos por exceso (estimar que es 55% cuando es 50%) se compensarán con las que nos equivoquemos por defecto (estimar que es 45% cuando es 50%).
A todo esto hay que sumar el hecho de que las estadísticas son una ayuda a la toma de decisiones pero no siempre nos van a dar exáctamente el movimiento correcto. Por ejemplo, para hacer una 3a bet light (y fold a una 4a por que llevamos una mierda) necesitas mucha fiabilidad en la estadística de fold to 3a bet. Pero no todos los movimientos que haces están basados en situaciones tan directas de EV. A veces te basta con saber que un jugador es agresivo, que llega poco al SD, ... sin saber el número exaxto para jugar las manos de una forma u otra.
En fin, la conclusión a la que quería llegar es que tienes razón en que se necesitan muchísimos casos de una estadística para que sea fiable. Y que para tener ese número de casos en una estadística se necesitan muchísimas manos de un jugador. Pero la necesidad de tener esa seguridad se da en casos muy concretos y los errores que puedes cometer a la larga se igualan. Además, la mayoría de información que se utiliza se hace de forma tendencial y para eso, con muestras para una determinada estadística de más de 100 casos vas muy sobrado. Yo, todo lo que está hecho con más de 50 casos ya le doy mucho crédito. Y estoy seguro de que muchos jerifantes de grandes compañías toman decisiones que hacen ganar o perder millones de € con menos seguridad con la que yo hago una 3a bet light 😉
16 años
1.792
17 años
3.872
Luzipher, buenas reflexiones. Creo que es muy útil que todos pensemos en la fiablidad de las estadísticas que utilizamos. Pero la verdad es que cuesta mucho hablar de estos temas sin liar más de lo que se aclara.
Lo que no veo es la necesidad de relacionar las manos totales de un jugador con la fiablidad de una estadística concreta. Para saber si esa estadística es fiable deberíamos fijarnos en las manos que tenemos de ella. En el PT por ejemplo, si pones el puntero del ratón encima de una te dice sobre cuantas manos está hecha. Esa en la "n" que deberíamos fijarnos.
Usando las probabilidades de muestreo, basadas en las formulas que has puesto, sabemos que tendremos un intervalo del 5% cuando (por ejemplo para el VP$IP):
- Para un VP$IP del 50%, el intervalo será de 45%-55% a partir de una muestra de 400.
- Para un VP$IP del 20%, el intervalo será de 15%-25% a partir de una muestra de 235.
-Para un VP$IP del 80%, el intervalo será de 75%-85% a partir de una muestra de 235 (un porcentaje de (x) y de (1-x) generan el mismo intervalo de confianza).
- Para un VP$IP del 10%, el intervalo será de 5%-15% a partir de una muestra de 138.
Hay que tener en cuenta que dentro del intervalo generado no todos los puntos tienen la misma probabilidad de darse. Así, para el primer caso es mucho más probable que el VP$IP sea realmente del 50% que del 45% (normalidad en los intervalos).
Tambien hay que pensar que este es el intervalo para evaluar 1 estadística de 1 persona y que en el largo plazo evaluaremos miles de estadísticas de miles de personas. Por tanto las veces que nos equivoquemos por exceso (estimar que es 55% cuando es 50%) se compensarán con las que nos equivoquemos por defecto (estimar que es 45% cuando es 50%).
A todo esto hay que sumar el hecho de que las estadísticas son una ayuda a la toma de decisiones pero no siempre nos van a dar exáctamente el movimiento correcto. Por ejemplo, para hacer una 3a bet light (y fold a una 4a por que llevamos una mierda) necesitas mucha fiabilidad en la estadística de fold to 3a bet. Pero no todos los movimientos que haces están basados en situaciones tan directas de EV. A veces te basta con saber que un jugador es agresivo, que llega poco al SD, ... sin saber el número exaxto para jugar las manos de una forma u otra.
En fin, la conclusión a la que quería llegar es que tienes razón en que se necesitan muchísimos casos de una estadística para que sea fiable. Y que para tener ese número de casos en una estadística se necesitan muchísimas manos de un jugador. Pero la necesidad de tener esa seguridad se da en casos muy concretos y los errores que puedes cometer a la larga se igualan. Además, la mayoría de información que se utiliza se hace de forma tendencial y para eso, con muestras para una determinada estadística de más de 100 casos vas muy sobrado. Yo, todo lo que está hecho con más de 50 casos ya le doy mucho crédito. Y estoy seguro de que muchos jerifantes de grandes compañías toman decisiones que hacen ganar o perder millones de € con menos seguridad con la que yo hago una 3a bet light 😉
Iniest
Lo que no veo es la necesidad de relacionar las manos totales de un jugador con la fiablidad de una estadística concreta. Para saber si esa estadística es fiable deberíamos fijarnos en las manos que tenemos de ella. En el PT por ejemplo, si pones el puntero del ratón encima de una te dice sobre cuantas manos está hecha. Esa en la "n" que deberíamos fijarnos.
De acuerdo, ese es el n correcto, cuando hablo de un factor para multiplicar la cantidad de manos es porque mi idea era llegar a una aproximación GENERAL de la cantidad de manos necesarias.
Iniest
Por tanto las veces que nos equivoquemos por exceso (estimar que es 55% cuando es 50%) se compensarán con las que nos equivoquemos por defecto (estimar que es 45% cuando es 50%).
Pero la necesidad de tener esa seguridad se da en casos muy concretos y los errores que puedes cometer a la larga se igualan.
Aqui es donde no estoy de acuerdo, los errores no se igualan en mi opinión. No estamos calculando un promedio y si algunas veces nos equivocamos por exceso como dices y otras por defecto entonces terminaremos compensando.
Tomamos decisiones basadas en una estadística, y si el valor es preciso, asumiendo que somos jugadores competentes entonces tomaremos la mejor decisión basándonos en ese número, pero la mejor decisión para ese número no necesariamente es la misma que para otro aunque sea un valor relativamente cercano, porque si tenemos un error, ya sea por defecto o por exceso eso nos hace tomar decisiones que se alejan de lo óptimo, pero ocurre en AMBOS escenarios y no se compensa, ambos errores se suman.
Saludos.
17 años
37
Solo comentar que es un lujo leeros. He estado haciendo un estudio y me he encontrado con todos estos problemas (que bien me habría ido leer este post). En breve publicaré los desastrosos resultados aunque seguiré batallando y empezaré por hacer una buena selección de atributos y valores asociados a ellos (manos que necesito de cada atributo para fiarme) por lo que este thread me va de lujo. Lo estudiaré en detalle y sacaré conclusiones.
Muchas gracias 😄
20 años
132
Las estadísticas están muy bien pero hay jugadores que cambian de estilo y tener una base de datos mastodontica de 6 meses es peligroso. Además los que juegan multitabla como robots no ven como un nit anda con tilt en alguna mesa.
17 años
37
Una pregunta.
¿Sabéis como se hace para ver los muestreos que hay (la dichosa n) en el Holdem Manager (cuando analizas la pestaña players)?
Muchas gracias 😄
16 años
41
Me ha gustado mucho el hilo, felicidades a luzipher, es fenomenal leer sobre estos temas, sobre todo teniendo en cuenta que soy lego en estadística.
Por si no he sacado las conclusiones correctas, las voy a poner y me corrijan si no están bien.
Stats que casi cada mano que jugamos nos da una muestra (ej: Vpip / PFR).
- 100 manos nos da una idea a grandes rasgos.
- 500 a 1.000 manos podemos empezar a confiar.
Stats que nos pueden dar una muestra valida cada 10 manos (ej: stats de steal).
- 1.000 manos nos da una idea a grandes rasgos.
- 10.000 manos podemos empezar a confiar.
Stats que nos dan una muestra valida cuando les parece bien (ej: 3-bet)
- 7.000 a 10.000 manos para el extremo inferior
- 4.000 manos para el extremo superior (9%)
Resumiendo, los stats nos dan una aproximación muy relativa, para tomar las decisiones, debemos utilizar las impresiones que nos da el conjunto de de los mismos, utilizar los más habituales (Vpip / PFR),las notas que tengamos, la historia en la mesa, las cartas que llevamos, etc.
Luzipher, supongo que si cito el hilo en algún post, no te importara. En caso contrario dímelo y no lo hare.
Responder
¿Quieres participar?
Inicia sesión o crea tu cuenta gratis para formar parte de la comunidad de Poker-Red.