El peso de la varianza en los Cash Games

Continuamos la serie de articulos cortos sobre la varianza en el poker. En esta ocasión nos centramos en la variante con menos impacto, los cash games, única modalidad en la que tenemos la posibilidad de jugar con stacks profundos de forma regular. Recuerda que puedes leer la introducción a la varianza en el poker en nuestro primer artículo de la serie.
En los cash games el nivel de ciegas es constante, es decir, se repiten exactamente las mismas situaciones a lo largo del tiempo. Las ev BB/100 son las ciegas que te corresponde ganar por cada 100 manos jugadas, en valor esperado (ev).
Es el indicador que permite estudiar el impacto de la varianza de manera óptima pero no significa que sea el mejor indicador para medir nuestros resultados globales, ya que entran en juego más factores, como el número de manos.
Por ejemplo, en una mesa de NL100 (Ciegas 0,5/1€) un jugador que gana a 10 evBB/100 en 5.000 manos, jugando solo una mesa, conseguirá unos beneficios mensuales de 500€ al mes, mientras que uno que abra más mesas simultáneamente y juegue 50.000 manos al mes, con un winrate de 5 BB/100, estará ganando 2.500€ al mes.
Como vemos, el jugador uno en nuestro ejemplo es más habilidoso que el dos, pero el sueldo por hora del segundo es mucho mayor.
El primer paso para hacer un análisis de varianza es conocer nuestra habilidad como jugadores de forma fiable, es decir, en una muestra de manos representativa.
El segundo factor a tener en cuenta es la desviación típica en BB/100, unos parámetros estándar son:
- NLH full ring: 60-80 BB/100
- NLH 6-max: 75-120 BB/100
- PLO full ring: 100-140 BB/100
- PLO 6-max: 120-160 BB/100
Por tanto, al ser la varianza el cuadrado de la desviación típica, podemos concluir que cuantos menos jugadores por mesa, más varianza y que en el Pot Limit Omaha tiene más peso que en NLHoldem. El ejemplo perfecto de estos dos factores acabamos de vivirlo en uno de los temas candentes de actualidad, el Galfond Challenge, un enfrentamiento heads up y en Pot Limit Omaha, de ahí los grandes swings que hemos visto.
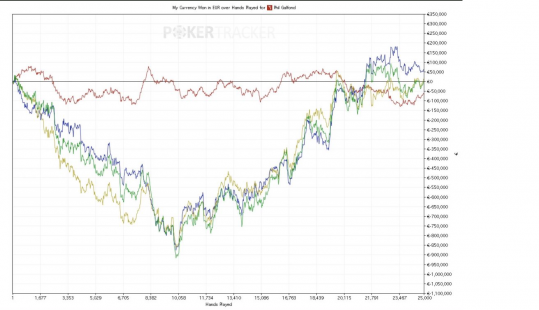
Para realizar nuestro análisis utilizaremos un valor de 100 bb/100 en la calculadora gratuita de varianza disponible en la página web Primedope
Vamos a realizar tres:
- Jugador que gana a 2,5 Ev bb/100
- Ganador a 6 Ev bb/100
- Crusher a 11 Ev bb/100.
Cada vez que realizamos un análisis de los posibles resultados, el programa nos dibuja una gráfica similar a esta, para explicarlo, utilizamos el ejemplo de nuestro tercer jugador en una muestra de 100.000 manos.
Un factor que suele escaparse a los jugadores es el hecho de que no solo los resultados finales están influidos por la varianza, el valor esperado también. Un ejemplo sencillo, acabamos all in en preflop con KsKc y nos pagan con AdAc. Nuestra mano en esta situación en concreto generará ev negativo, pero la mayoría de veces no. Esto mismo sucede postflop, es decir, la distribución de cartas que recibamos tanto nosotros como nuestro rival está marcada por la varianza. Es importante tener confianza en nuestro juego y conseguir una muestra importante de manos para que este factor converja.
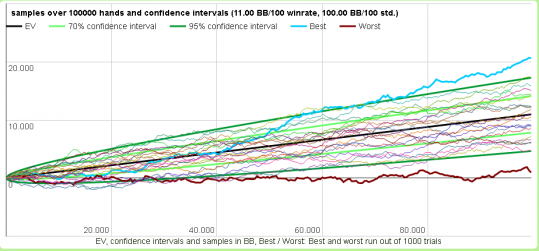
Como vemos, la gráfica tiene límite superior e inferior, de color azul y marrón. Es el abanico de posibles resultados a los que nos enfrentamos, el mejor y el peor caso posible, incluyendo los resultados más dispersos (el 5% menos probable).
La línea negra representa el valor esperado (ev), la media esperada en función de nuesrra habilidad.
Las líneas de color verde oscuro reflejan nuestros posibles resultados con un intervalo de confianza del 95%, mientras que las verdes claras al 70% de confianza. Esto significa que en un 95% y 70% de probabilidad nuestros resultados se encontrarán en un punto entre estas líneas.
Comparamos los resultados de los tres jugadores en muestras de 1.000 y 100.000 manos.
| Ev BB | 95% Intervalo de Confianza 1.000 manos | 95% Intervalo de Confianza 100.000 manos | Probabilidad de perder tras 1.000 manos | Probabilidad de perder tras 100.000 manos | Bankroll Mínimo menos 5% bustear |
|---|---|---|---|---|---|
| 2.5 BB/100 | [-607 BB, 657 BB] [-60.75 BB/100, 65.75 BB/100] | [-3825 BB, 8825 BB] [-3.82 BB/100, 8.82 BB/100] | 46.85% | 21.46% | 5991 BB (59,91 buy ins) |
| 6 BB/100 | [-572 BB, 692 BB] [-57.25 BB/100, 69.25 BB/100] | [-325 BB, 12325 BB] [-0.32 BB/100, 12.32 BB/100] | 42.47% | 2.89% | 2496 BB (24,96 buy ins) |
| 11 BB/100 | [-522 BB, 742 BB] [-52.25 BB/100, 74.25 BB/100] | [4675 BB, 17325 BB] [4.68 BB/100, 17.32 BB/100] | 36.40% | 0.02% | 1362 BB (13,62 buy ins) |
*Un intervalo de 95% confianza significa que en nuestro primer ejemplo, los resultados están entre -607BB (perder 6 buy ins del nivel) y 657BB (ganar 6 buy ins y medio) el 95% de las veces.
Como apreciamos en la tabla, cuanto más grande sea la muestra, menor será el impacto de la varianza y cuanto mayor sea nuestra habilidad en las mesas, menor probabilidad de perder dinero en la misma muestra (número de manos).
Como veremos más adelante, estos vaivenes son relativamente pequeños en comparación al resto de modalidades de poker. En el siguiente artículo nos centraremos en el opuesto, la modalidad con resultados más variables, los torneos multimesa.
Todavía no se ha realizado ningún comentario en esta noticia.
¿Quieres participar?
Es fácil y no te costará nada
¡únete a Poker-Red!