Poker I+D: Fiabilidad de los valores del HUD

Siempre que tomamos una decisión cuando estamos sentados en una mesa de poker, solemos hacerlo tomando como base algún dato estadístico que nos proporciona el HUD. En muchos de estos casos, se hace tomando como “fiable” un dato que ni remotamente lo es y que, por tanto, nos está induciendo a cometer una gran cantidad de errores.
En EducaPoker hemos construido recientemente una estrategia explotadora Multistack que se basa en gran medida en la interpretación de estadísticas. De ahí surge la idea de hacer un estudio de la fiabilidad de los datos estadísticos que nos ofrece el HUD y así saber cuándo resulta o no fiable tomar decisiones en base a estos datos.
¿Qué es un dato en el HUD?
Un valor que obtenemos en el HUD es una muestra que nos indica la cantidad de veces que ha sucedido un evento determinado.
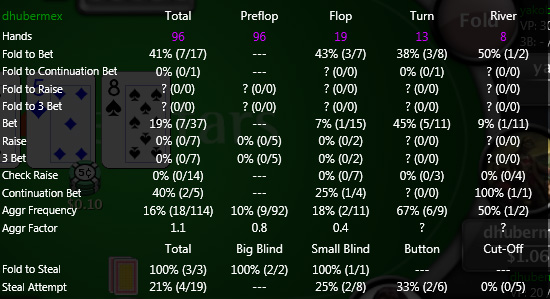
Por ejemplo, cuando tenemos que un rival ha abierto 35 veces en CO de un total de 120 casos, vemos un 29 (35/120) que representa que el evento determinado --que el rival abra una mano limpia en CO- ha sucedido en un 29% de casos.
¿Cómo medir la fiabilidad?
Matemáticamente, una distribución binomial es una distribución que mide el número de sucesos independientes en una secuencia de ensayos; es decir, se ajusta a nuestro modelo. Podemos leer más sobre la distribución binomial en la Wikipedia.
Una vez hemos tomado nuestra muestra como una muestra de una distribución binomial, podemos calcular intervalos de confianza y fiabilidad de estos intervalos.
Un intervalo de confianza es el intervalo donde esperamos que se encuentre el valor real. La probabilidad del intervalo es la probabilidad que tenemos de que el valor real se encuentre dentro de dicho intervalo.
Para una distribución binomial, podemos calcular su intervalo de confianza conociendo el tamaño de la muestra y la fiabilidad que queremos del intervalo.
Si te interesa profundiar en el tema, puedes leer más acerca de intervalos de confianza en distribuciones binomiales aquí.
¿Qué fiabilidad necesitamos?
Hemos escogido una fiabilidad relativamente baja, ya que cuando estamos jugando es mejor usar una información que será precisa una cantidad razonable de veces que no usar ninguna información.
Por ello, hemos asumido una fiabilidad del intervalo del 75%. Es decir, una de cada cuatro veces el valor real de nuestro rival estará fuera del intervalo.
¿Qué precisión necesitamos?
La precisión que necesitamos no es igual para todos los datos.
Por ejemplo, si de un oponente tengo un VPIP del 75, probablemente un error de ± 20 sea tolerable. Jugaré de forma muy parecida tanto si el VPIP del oponente es un 55 o si es un 75. Pero si, en cambio, hablamos de datos como el 3bet en BTN, necesitamos un intervalo mucho más estrecho en valor absoluto.
Así, un 3bet de un 7% ± 5 no tiene mucho sentido, ya que un 3bet de un 3 no tiene nada que ver con un 3bet de un 11.
La precisión que necesitamos depende en gran medida del propio dato.
¿Qué tamaño de muestra necesitamos?
El tamaño de muestra necesario depende de varios factores.
- El intervalo de confianza escogido
- La fiabilidad de este intervalo de confianza
- El valor medio del dato que queremos medir.
Hemos determinado que una fiabilidad del 75% será suficiente para nosotros. Veamos cómo afectan los distintos factores al tamaño de la muestra en los siguientes casos.
| Casos por valor para una fiabilidad del 75% | |||
|---|---|---|---|
| Valor medio del dato HUD | ± 2% | ± 5% | ± 10% |
| Valor medio 5 | 158 | 26 | |
| Valor medio 10 | 298 | 48 | 12 |
| Valor medio 15 | 422 | 68 | 17 |
| Valor medio 25 | 620 | 100 | 25 |
| Valor medio 50 | 828 | 133 | 34 |
Para un dato como el WWSF, cuyo valor promedio se acerca al 50, vemos que para tener una precisión de ± 2 necesitamos 828 casos. En datos como el WWSF, necesitamos esta precisión ya que una diferencia de 5 puntos es muy relevante.
Para datos como el Fold al Cbet, por ejemplo, que también oscilan el 50%, nos puede servir una precisión de ± 5. En ese caso necesitaríamos un tamaño de muestra de unos 133 casos.
Para datos como el 4bet, que suelen rondar un 15% de valor medio, necesitamos una fiabilidad de un ± 2. Esto implica que necesitamos una muestra con 422 casos de 4bet.
Es muy importante señalar que el tamaño de muestra necesaria para cada dato no está relacionado con el número de manos de un oponente. De un rival podemos tener 1000 manos pero solo 70 casos de situaciones en los que ha podido hacer 4bet.
La muestra necesaria
Ahora ya hemos visto cuántos casos necesitaremos para que un dato resulte fiable, teniendo en cuenta que no hemos sido demasiado estrictos con dicha fiabilidad.
Como podemos observar, la mayoría de los casos en los que nos basamos para tomar decisiones rara vez tienen la muestra necesaria para que resulten fiables.
La mayoría de trackers nos muestran la cantidad de casos que tenemos de cada dato estadístico, pero no resulta muy difícil hacer una estimación de la cantidad de manos total necesaria para que se den estos casos.
Basándonos en una base de datos gigantesca, hemos hecho una estimación de la cantidad de manos necesaria para un determinado suceso. Destacar que cada entorno puede variar tremendamente estas muestras.
| OR pos | vs 3b after R | 3b after R in BTN | vs OR | vs OR in BTN | vs 4b after 3b |
|---|---|---|---|---|---|
| 12,71 | 49,96 | 144,18 | 2,99 | 14,61 | 213,76 |
Como podemos observar, un open raise sucede bastante a menudo, pero un 4bet posicional no tanto.
Viendo algunos ejemplos de valores postflop la cosa no mejora demasiado.
| WWSF | W$SD | (F) Cbet | (F) Cbet IP |
|---|---|---|---|
| 5,84 | 20,61 | 13,00 | 26,05 |
Ahora, traslademos estos datos del ejemplo a los datos que hemos obtenidos anteriormente y tendremos una aproximación sobre la cantidad de manos necesaria para que un dato sea fiable.
A modo de ejemplo, un OR por posiciones con una media cercana al 50 necesitaría una fiabilidad de ± 10% para ser útil. Multiplicando los casos por mano (12,71) por la cantidad necesaria para llegar a la fiabilidad que nos interesa (34), tenemos que con unas 500 manos estos datos comienzan a aportarnos datos bastante fiables.
Si los datos muy generales necesitan muestras amplias para resultar fiables, imaginad la muestra necesaria para datos como el 5bet o los datos en el turn de 3b pots.
El entorno y la muestra
Un último apunte a realizar sería que el entorno en que juguemos también influye en la cantidad de casos por mano que se dan en función del tipo de dato.
Por ejemplo, en un entorno agresivo, que apenas defienda las ciegas haciendo call, tendremos muchísimos menos casos por mano de datos defensivos postflop que en otro entorno en el que ocurra todo lo contrario.
Conclusión
Tras realizar el estudio, la conclusión más obvia a la que llegamos es que, muchas veces, estamos tomando decisiones en base a datos que para nada son fiables y a causa de esto cometemos errores muy graves que repercuten en nuestros beneficios.
Cuando estés en las mesas, quieras tomar una decisión en base a un dato y tengas pocas muestras, piénsalo dos veces. En la mayoría de las ocasiones estarás cometiendo un error.
Todavía no se ha realizado ningún comentario en esta noticia.
¿Quieres participar?
Es fácil y no te costará nada
¡únete a Poker-Red!